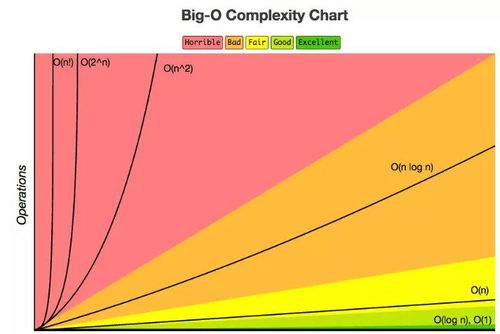
算法的时间复杂度
2020/12/16 20:25:30
本文主要是介绍算法的时间复杂度,对大家解决编程问题具有一定的参考价值,需要的程序猿们随着小编来一起学习吧!
算法的时间与空间复杂度
事后分析法
缺点:不同的数据规模,不同的机器下算法运行的时间不同,无法做到计算运行时间
事前分析法
大O时间复杂度
渐进时间复杂度 随着n的增长,程序运行时间跟随n变化的趋势
几个原则
去掉常数项
2(n^2) =n^2
一段代码取时间复杂度最高的
test(n) {
//时间复杂度n^3
for(int i = 0; i < n ; i++){
for(int i = 0; i < n ; i++){
for(int i = 0; i < n ; i++){
print(n);
}
}
}
//时间复杂度n^2
for(int i = 0; i < n ; i++){
for(int i = 0; i < n ; i++){
print(n);
}
}
//时间复杂度n
for(int i = 0; i < n ; i++){
print(n);
}
}
这段代码的时间复杂度为n3+n2+n
当n足够大时,n2和n与n3相比太小,可以忽略不计
常见复杂度
o(1)
i = i + 1;
o(n)
test(n){
for(int i = 0 ;i < n;i++){
print(i);
}
}
o(n^2)
test(n){
for(int i = 0 ;i < n;i++){
print(i);
for(int j = 0 ;j < n;j++){
print(i);
}
}
}
o(log2n)
PS:如果ax =N(a>0,且a≠1),那么数x叫做以a为底N的对数,记作x=logaN,读作以a为底N的,其中a叫做对数的底数,N叫做真数。
test(n) {
int i = 1;
while (i <= n) {
i = 2 * i;
}
}
随着循环次数的增加,i的值变化如下
根据对数函数的公式 2的i次方等于n,i等于log2n
最好情况时间复杂度
数据比较有序的情况的时间复杂度
最坏情况时间复杂度
数据完全无序
空间复杂度
与n无关的代码空间复杂度可以忽略
空间复杂度O(n)
test(n) {
//在内存中开辟了一个长度为n的数组
List array = List(n);
print(array.length);
}
如果你对Dart flutter 计算机基础感兴趣可以关注作者,持续分享优质文章
坐而论道不如起而行之
这篇关于算法的时间复杂度的文章就介绍到这儿,希望我们推荐的文章对大家有所帮助,也希望大家多多支持为之网!
- 2024-01-18android.permission.read_media_video
- 2024-01-18android_getaddrinfo failed eai_nodata
- 2024-01-18androidmo
- 2024-01-15Android下三种离屏渲染技术
- 2024-01-09Android 蓝牙使用
- 2024-01-06Android对接华为AI - 文本识别
- 2023-11-15代码安全之代码混淆及加固(Android)
- 2023-11-10简述Android语音播报TTS
- 2023-11-06Android WiFi工具类
- 2023-07-22Android开发未来的出路