『数据结构与算法』二叉查找树(BST)
2020/12/21 8:07:26
本文主要是介绍『数据结构与算法』二叉查找树(BST),对大家解决编程问题具有一定的参考价值,需要的程序猿们随着小编来一起学习吧!
GitHub源码分享
主页地址:/gozhuyinglong.github.io
源码分享:github.com/gozhuyinglong/blog-demos
1. 二叉查找树(Binary Search Tree)
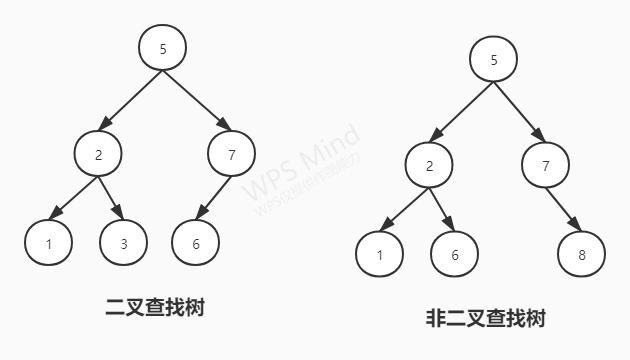
二叉查找树又叫二叉排序树(Binary Sort Tree),或叫二叉搜索树,简称BST。BST是一种节点值之间有次序的二叉树。其特性是:
- 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若任意节点的右子树不空,则右子树上所有节点的值均大于或等于它的根节点的值;
- 任意节点的左、右子树也分别为二叉查找树;
二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低,为O(logN)O(logN)O(logN)。用大OOO符号表示的时间复杂度:
| 算法 | 平均 | 最差 |
|---|---|---|
| 空间 | O(N)O(N)O(N) | O(N)O(N)O(N) |
| 搜索 | O(logN)O(logN)O(logN) | O(N)O(N)O(N) |
| 插入 | O(logN)O(logN)O(logN) | O(N)O(N)O(N) |
| 删除 | O(logN)O(logN)O(logN) | O(N)O(N)O(N) |
2. BST的实现
二叉查找树要求所有的节点元素都能够排序,所以我们的Node节点类需要实现Comparable接口,树中的两个元素可以使用compareTo方法进行比较。
我们节点中元素的类型为int型,所以该接口泛型为Comparable<Integer>,下面是具体实现:
2.1 节点类
- element 为数据元素
- left 为左子节点
- right 为右子节点
class Node implements Comparable<Integer> {
private final int element; // 数据元素
private Node left; // 左子树
private Node right; // 右子树
private Node(Integer element) {
this.element = element;
}
@Override
public int compareTo(Integer o) {
return o.compareTo(element);
}
}
2.2 二叉查找树类
- root 为树根,所有的操作均始于此
后面会在该类中增加其他方法,如添加、查找、删除等
class BinarySearchTree {
private Node root; // 树根
}
3. 插入节点
向二叉查找树中插入的节点总是叶子节点,插入过程如下:
- 若
root为空,则将插入节点设为root - 当前元素与插入元素通过
compareTo进行比较,若插入元素值小,并且左子节点left为空,则插入至当前节点左子节点;否则继续递归 - 若插入元素值大,且右子节点
right为空,则插入至当前节点右子节点;否则继续递归。 - 若插入元素等于当前节点元素,则插入失败。注:也可以将其插入到右子节点,我这里为了方便直接放弃插入。
具体实现:
在BinarySearchTree类中添加两个方法:
public boolean add(int element)为公开方法private boolean add(Node node, int element)为私有方法,内部递归使用
// 添加元素
public boolean add(int element) {
if (root == null) {
root = new Node(element);
return true;
}
return add(root, element);
}
// 添加元素(递归)
private boolean add(Node node, int element) {
if (node.compareTo(element) < 0) {
if (node.left == null) {
node.left = new Node(element);
return true;
} else {
return add(node.left, element);
}
} else if (node.compareTo(element) > 0) {
if (node.right == null) {
node.right = new Node(element);
return true;
} else {
return add(node.right, element);
}
} else {
return false;
}
}
4. 查找节点
通过二叉查找树查找元素,其过程如下:
- 若
root为空,则查找失败 - 将当前元素与目标元素对比,若相等则查找成功。
- 若不相等,则继续递归查找:若目标值小于当前节点值,则查找左子树;否则,查找右子树。
具体实现:
在BinarySearchTree类中添加两个方法:
public Node find(int element)为公开方法private Node find(Node node, int element)为私有方法,内部递归使用
// 查找元素
public Node find(int element) {
if (root == null) {
return null;
}
return find(root, element);
}
// 查询元素(递归)
private Node find(Node node, int element) {
if (node == null) {
return null;
}
int compareResult = node.compareTo(element);
if (compareResult < 0) {
return find(node.left, element);
} else if (compareResult > 0) {
return find(node.right, element);
} else {
return node;
}
}
5. 遍历节点
BST是一个有序二叉树,通过中序遍历可顺序输出树中节点。
中序遍历过程如下:
- 递归遍历左子节点
- 输出当前节点
- 递归遍历右子节点
具体实现:
在BinarySearchTree类中添加两个方法:
public void orderPrint()为公开方法private void orderPrint(Node node)为私有方法,内部递归使用
// 遍历节点
public void orderPrint() {
orderPrint(root);
}
// 遍历节点(递归)
private void orderPrint(Node node) {
if (node == null) {
return;
}
// 递归左子节点
if (node.left != null) {
orderPrint(node.left);
}
// 输出当前节点
System.out.println(node.element);
// 递归右子节点
if (node.right != null) {
orderPrint(node.right);
}
}
6. 删除节点
删除节点最为复查,共有三种情况:
6.1 目标元素为叶子节点
叶子节点最容易删除,过程如下:
- 找到目标节点的父节点
- 判断目标节点是父节点的左子树还是右子树
- 若是左子树,将父节点的
left设为空;否则将父节点的right设为空
6.2 目标元素即有左子树,也有右子树
该情况删除操作最为复杂,过程如下:
- 找到目标节点的父节点
- 判断目标节点是父节点的左子树还是右子树
- 找到右子树中最小元素(叶子节点),将其赋给临时变量
minNode,再将该元素从树中删除 - 将目标元素的属性赋予
minNode。 - 若目标元素是父节点的左子树,将父节点的
left设为minNode;否则将父节点的right设为minNode
6.3 目标元素只有左子树,或只有右子树
删除过程如下
- 找到目标节点的父节点
- 判断目标节点是父节点的左子树还是右子树
- 若是左子树,将父节点的
left设为目标节点不为空的子树;否则将父节点的right设为目标节点不为空的子树
具体实现
在BinarySearchTree类中添加两个方法:
public boolean remove(int element)为公开方法private boolean remove(Node parentNode, Node node, int element)为私有方法,内部递归使用
// 删除节点
public boolean remove(int element) {
if (root == null) {
return false;
}
// 如果删除的元素是root
if (root.compareTo(element) == 0) {
if (root.right == null) {
root = root.left;
} else {
root.right.left = root.left;
root = root.right;
}
return true;
}
return remove(null, root, element);
}
// 删除节点(递归)
private boolean remove(Node parentNode, Node node, int element) {
if (node == null) {
return false;
}
// 先找到目标元素
int compareResult = node.compareTo(element);
if (compareResult < 0) {
return remove(node, node.left, element);
}
if (compareResult > 0) {
return remove(node, node.right, element);
}
// 找到目标元素,判断该节点是父节点的左子树还是右子树
boolean isLeftOfParent = false;
if (parentNode.left != null && parentNode.left.compareTo(element) == 0) {
isLeftOfParent = true;
}
// 删除目标元素
if (node.left == null && node.right == null) { // (1)目标元素为叶子节点,直接删除
if (isLeftOfParent) {
parentNode.left = null;
} else {
parentNode.right = null;
}
} else if (node.left != null && node.right != null) { // (2)目标元素即有左子树,也有右子树
// 找到右子树最小值(叶子节点),并将其删除
Node minNode = findMin(node.right);
remove(minNode.element);
// 将该最小值替换要删除的目标节点
minNode.left = node.left;
minNode.right = node.right;
if(isLeftOfParent) {
parentNode.left = minNode;
} else {
parentNode.right = minNode;
}
} else { // (3)目标元素只有左子树,或只有右子树
if (isLeftOfParent) {
parentNode.left = node.left != null ? node.left : node.right;
} else {
parentNode.right = node.left != null ? node.left : node.right;
}
}
return true;
}
}
7. 完整代码
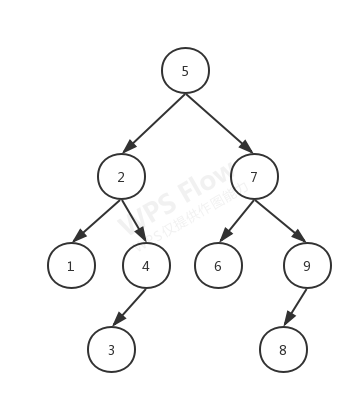
该代码根据下图二叉查找树实现,其操作包括:添加、查找、遍历、删除、查询最小值、查询最大值。
public class BinarySearchTreeDemo {
public static void main(String[] args) {
BinarySearchTree tree = new BinarySearchTree();
System.out.println("----------------------添加元素");
Integer[] array = {5, 2, 7, 1, 4, 3, 7, 6, 9, 8};
for (Integer element : array) {
System.out.printf("添加元素[%s] --> %s\n", element, tree.add(element));
}
System.out.println("----------------------顺序输出(中序遍历)");
tree.orderPrint();
System.out.println("----------------------查找元素");
System.out.println(tree.find(7));
System.out.println("----------------------查找最小元素");
System.out.println(tree.findMin());
System.out.println("----------------------查找最大元素");
System.out.println(tree.findMax());
System.out.println("----------------------是否包含元素");
System.out.println("是否包含[0] --> \t" + tree.contains(0));
System.out.println("是否包含[2] --> \t" + tree.contains(2));
System.out.println("----------------------删除目标元素");
System.out.println("删除[0] --> \t" + tree.remove(0));
tree.orderPrint();
System.out.println("删除[1] --> \t" + tree.remove(1));
tree.orderPrint();
System.out.println("删除[4] --> \t" + tree.remove(4));
tree.orderPrint();
System.out.println("删除[7] --> \t" + tree.remove(7));
tree.orderPrint();
}
private static class BinarySearchTree {
private Node root; // 树根
/**
* 添加元素
*
* @param element
* @return
*/
public boolean add(int element) {
if (root == null) {
root = new Node(element);
return true;
}
return add(root, element);
}
/**
* 添加元素(递归)
*
* @param node
* @param element
* @return
*/
private boolean add(Node node, int element) {
if (node.compareTo(element) < 0) {
if (node.left == null) {
node.left = new Node(element);
return true;
} else {
return add(node.left, element);
}
} else if (node.compareTo(element) > 0) {
if (node.right == null) {
node.right = new Node(element);
return true;
} else {
return add(node.right, element);
}
} else {
return false;
}
}
/**
* 查询元素
*
* @param element
* @return
*/
public Node find(int element) {
if (root == null) {
return null;
}
return find(root, element);
}
/**
* 查询元素(递归)
*
* @param node
* @param element
* @return
*/
private Node find(Node node, int element) {
if (node == null) {
return null;
}
int compareResult = node.compareTo(element);
if (compareResult < 0) {
return find(node.left, element);
} else if (compareResult > 0) {
return find(node.right, element);
} else {
return node;
}
}
/**
* 查找最大值
*
* @return
*/
public Node findMax() {
return findMax(root);
}
/**
* 查找最大值(递归)
*
* @param node
* @return
*/
private Node findMax(Node node) {
if (node.right == null) {
return node;
}
return findMax(node.right);
}
/**
* 查找最小值
*
* @return
*/
private Node findMin() {
return findMin(root);
}
/**
* 查找最小值(递归)
*
* @param node
* @return
*/
private Node findMin(Node node) {
if (node.left == null) {
return node;
}
return findMin(node.left);
}
/**
* 顺序输出
*/
public void orderPrint() {
orderPrint(root);
}
/**
* 顺序输出(递归)
*
* @param node
*/
private void orderPrint(Node node) {
if (node == null) {
return;
}
// 递归左子节点
if (node.left != null) {
orderPrint(node.left);
}
// 输出当前节点
System.out.println(node.element);
// 递归右子节点
if (node.right != null) {
orderPrint(node.right);
}
}
/**
* 是否包含某值
*
* @param element
* @return
*/
public boolean contains(int element) {
if (find(element) == null) {
return false;
}
return true;
}
/**
* 删除目标元素
*
* @param element
* @return
*/
public boolean remove(int element) {
if (root == null) {
return false;
}
// 如果删除的元素是root
if (root.compareTo(element) == 0) {
if (root.right == null) {
root = root.left;
} else {
root.right.left = root.left;
root = root.right;
}
return true;
}
return remove(null, root, element);
}
/**
* 删除目标元素(递归),有三种情况:
* (1)目标元素为叶子节点
* (2)目标元素即有左子树,也有右子树
* (3)目标元素只有左子树,或只有右子树
*
* @param parentNode 当前节点的父节点
* @param node 当前节点(若当前节点上的元素与要删除的元素匹配,则删除当前节点)
* @param element 要删除的元素
* @return
*/
private boolean remove(Node parentNode, Node node, int element) {
if (node == null) {
return false;
}
// 先找到目标元素
int compareResult = node.compareTo(element);
if (compareResult < 0) {
return remove(node, node.left, element);
}
if (compareResult > 0) {
return remove(node, node.right, element);
}
// 找到目标元素,判断该节点是父节点的左子树还是右子树
boolean isLeftOfParent = false;
if (parentNode.left != null && parentNode.left.compareTo(element) == 0) {
isLeftOfParent = true;
}
// 删除目标元素
if (node.left == null && node.right == null) { // (1)目标元素为叶子节点,直接删除
if (isLeftOfParent) {
parentNode.left = null;
} else {
parentNode.right = null;
}
} else if (node.left != null && node.right != null) { // (2)目标元素即有左子树,也有右子树
// 找到右子树最小值(叶子节点),并将其删除
Node minNode = findMin(node.right);
remove(minNode.element);
// 将该最小值替换要删除的目标节点
minNode.left = node.left;
minNode.right = node.right;
if(isLeftOfParent) {
parentNode.left = minNode;
} else {
parentNode.right = minNode;
}
} else { // (3)目标元素只有左子树,或只有右子树
if (isLeftOfParent) {
parentNode.left = node.left != null ? node.left : node.right;
} else {
parentNode.right = node.left != null ? node.left : node.right;
}
}
return true;
}
}
private static class Node implements Comparable<Integer> {
private final Integer element; // 数据元素
private Node left; // 左子树
private Node right; // 右子树
private Node(Integer element) {
this.element = element;
}
@Override
public int compareTo(Integer o) {
return o.compareTo(element);
}
@Override
public String toString() {
return "Node{" +
"element=" + element +
'}';
}
}
}
输出结果:
----------------------添加元素
添加元素[5] --> true
添加元素[2] --> true
添加元素[7] --> true
添加元素[1] --> true
添加元素[4] --> true
添加元素[3] --> true
添加元素[7] --> false
添加元素[6] --> true
添加元素[9] --> true
添加元素[8] --> true
----------------------顺序输出(中序遍历)
1
2
3
4
5
6
7
8
9
----------------------查找元素
Node{element=7}
----------------------查找最小元素
Node{element=1}
----------------------查找最大元素
Node{element=9}
----------------------是否包含元素
是否包含[0] --> false
是否包含[2] --> true
----------------------删除目标元素
删除[0] --> false
1
2
3
4
5
6
7
8
9
删除[1] --> true
2
3
4
5
6
7
8
9
删除[4] --> true
2
3
5
6
7
8
9
删除[7] --> true
2
3
5
6
8
9
这篇关于『数据结构与算法』二叉查找树(BST)的文章就介绍到这儿,希望我们推荐的文章对大家有所帮助,也希望大家多多支持为之网!
- 2024-11-24Java中定时任务实现方式及源码剖析
- 2024-11-24Java中定时任务实现方式及源码剖析
- 2024-11-24鸿蒙原生开发手记:03-元服务开发全流程(开发元服务,只需要看这一篇文章)
- 2024-11-24细说敏捷:敏捷四会之每日站会
- 2024-11-23Springboot应用的多环境打包入门
- 2024-11-23Springboot应用的生产发布入门教程
- 2024-11-23Python编程入门指南
- 2024-11-23Java创业入门:从零开始的编程之旅
- 2024-11-23Java创业入门:新手必读的Java编程与创业指南
- 2024-11-23Java对接阿里云智能语音服务入门详解