『数据结构与算法』二叉树
2020/12/21 8:07:26
本文主要是介绍『数据结构与算法』二叉树,对大家解决编程问题具有一定的参考价值,需要的程序猿们随着小编来一起学习吧!
GitHub源码分享
主页地址:/gozhuyinglong.github.io
源码分享:github.com/gozhuyinglong/blog-demos
1. 二叉树(Binary Tree)
二叉树是一棵特殊的[树],其结构简单但很重要。二叉树的特点是每个节点最多有两棵子树,并且有左右之分。
-
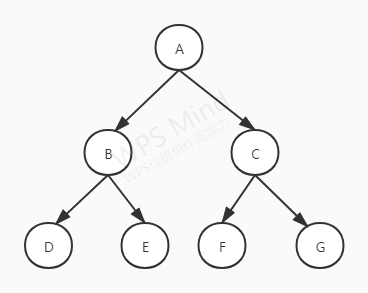
满二叉树
如果一棵二叉树的所有叶子节点都在最后一层,称为满二叉树。满二叉树的结点总数 = 2n−12^n-12n−1 (n为层数)。如下图二叉是的层数为3,其结点总数为23−1=72^3-1=723−1=7 -
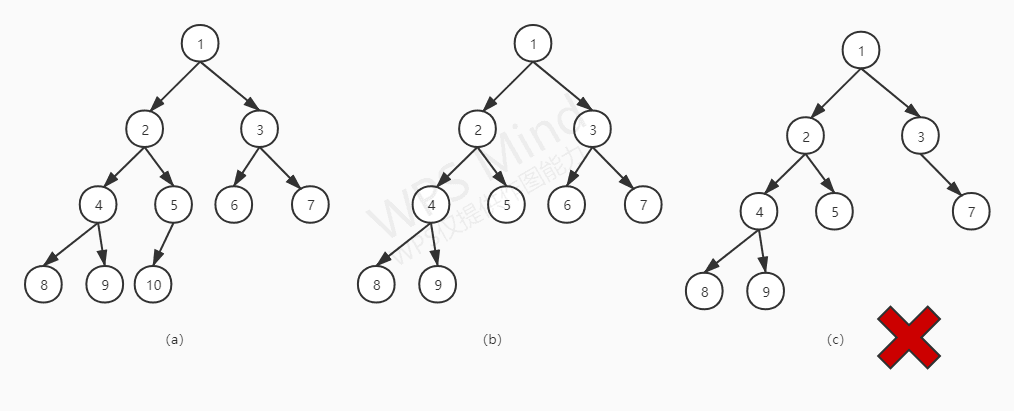
完全二叉树
一棵深度为k的有n个结点的二叉树,对树中的节点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。显示下图中a和b是完全二叉树,而c不是完全二叉树(倒数第二层不连续)
小结:一棵满二叉树一定是一棵完全二叉树;而一棵完全二叉树不一定是满二叉树。
2. 二叉树的五种形态
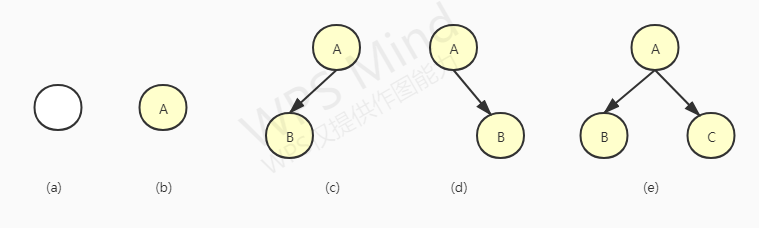
二叉树是递归定义的,其节点有左右子树之分,逻辑上二叉树有五种基本形态:
- 空二叉树(图a)
- 只有一个根节点的二叉树(图b)
- 只有左子树(图c)
- 只有右子树(图d)
- 完全二叉树(图e)
3. 二叉树的遍历(前序、中序、后序)
- 前序遍历:先输出父节点,再遍历左子树,最后遍历右子树。
- 中序遍历:先遍历左子树,再输出父节点,最后遍历右子树。
- 后序遍历:先遍历左子树,再遍历右子树,最后输出父节点。
小结:用输出父节点的顺序来判断是前序、中序还是后序遍历
4. 代码实现
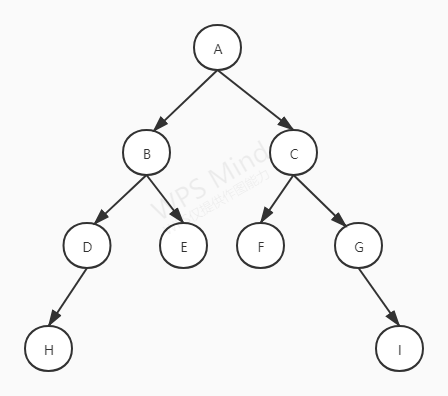
通过Java代码实现下图中二叉树,并通过三种方式遍历该二叉树(前序、中序、后序)。
Node类为节点类,其中element表示节点元素,left为左子节点,right为右子节点。
BinaryTree类实现二叉树的具体操作,如前序遍历、中序遍历、后序遍历。
public class BinaryTreeDemo {
public static void main(String[] args) {
BinaryTree tree = new BinaryTree();
Node a = new Node("A");
Node b = new Node("B");
Node c = new Node("C");
Node d = new Node("D");
Node e = new Node("E");
Node f = new Node("F");
Node g = new Node("G");
Node h = new Node("H");
Node i = new Node("I");
tree.setRoot(a);
a.left = b;
a.right = c;
b.left = d;
b.right = e;
d.left = h;
c.left = f;
c.right = g;
g.right = i;
System.out.println("---------------前序遍历");
tree.preOrder();
System.out.println("---------------中序遍历");
tree.inOrder();
System.out.println("---------------后序遍历");
tree.postOrder();
}
private static class BinaryTree {
private Node root; // 根
public void setRoot(Node root) {
this.root = root;
}
/**
* 前序遍历
*/
public void preOrder() {
preOrder(root, 0);
}
/**
* 前序遍历
*
* @param node
* @param depth 层级(用于辅助输出)
*/
public void preOrder(Node node, int depth) {
if (node == null) {
return;
}
// 输出当前节点
this.print(node, depth);
// 递归左子节点
if (node.left != null) {
preOrder(node.left, depth + 1);
}
// 递归右子节点
if (node.right != null) {
preOrder(node.right, depth + 1);
}
}
/**
* 中序遍历
*/
public void inOrder() {
inOrder(root, 0);
}
/**
* 中序遍历
*
* @param node
* @param depth 层级(用于辅助输出)
*/
public void inOrder(Node node, int depth) {
if (node == null) {
return;
}
// 递归左子节点
if (node.left != null) {
inOrder(node.left, depth + 1);
}
// 输出当前节点
this.print(node, depth);
// 递归右子节点
if (node.right != null) {
inOrder(node.right, depth + 1);
}
}
/**
* 后序遍历
*/
public void postOrder() {
postOrder(root, 0);
}
/**
* 后序遍历
*
* @param node
* @param depth 层级(用于辅助输出)
*/
public void postOrder(Node node, int depth) {
if (node == null) {
return;
}
// 递归左子节点
if (node.left != null) {
postOrder(node.left, depth + 1);
}
// 递归右子节点
if (node.right != null) {
postOrder(node.right, depth + 1);
}
// 输出当前节点
this.print(node, depth);
}
/**
* 按照层级输出节点元素
*
* @param node
* @param depth
*/
private void print(Node node, int depth) {
StringBuilder t = new StringBuilder();
for (int i = 0; i < depth; i++) {
t.append("\t");
}
System.out.printf("%s%s\n", t.toString(), node.element);
}
}
private static class Node {
private final Object element; // 节点元素
private Node left; // 左子节点
private Node right; // 右子节点
public Node(Object element) {
this.element = element;
}
}
}
输出结果:
---------------前序遍历 A B D H E C F G I ---------------中序遍历 H D B E A F C G I ---------------后序遍历 H D E B F I G C A
这篇关于『数据结构与算法』二叉树的文章就介绍到这儿,希望我们推荐的文章对大家有所帮助,也希望大家多多支持为之网!
- 2024-11-24Java中定时任务实现方式及源码剖析
- 2024-11-24Java中定时任务实现方式及源码剖析
- 2024-11-24鸿蒙原生开发手记:03-元服务开发全流程(开发元服务,只需要看这一篇文章)
- 2024-11-24细说敏捷:敏捷四会之每日站会
- 2024-11-23Springboot应用的多环境打包入门
- 2024-11-23Springboot应用的生产发布入门教程
- 2024-11-23Python编程入门指南
- 2024-11-23Java创业入门:从零开始的编程之旅
- 2024-11-23Java创业入门:新手必读的Java编程与创业指南
- 2024-11-23Java对接阿里云智能语音服务入门详解