『数据结构与算法』树

GitHub源码分享

主页地址：/gozhuyinglong.github.io
源码分享：github.com/gozhuyinglong/blog-demos

1. 前言

我们前面讲到了[数组]和[链表]两种数据结构，其各自有自己的优缺点，我们来回顾一下。

• 数组（Array）
  优点：通过下标访问速度非常快。
  缺点：需要检索具体某个值时，或者插入值时（会整体移动）效率较低

• 链表（Linked List）
  优点：在插入某个值时，效率比数组高
  缺点：检索某个值时效率仍然较低

我们本篇讲到的树，便能提高数据的存储和读取效率。

2. 树（Tree）

树是一种非线性的数据结构，它包含n(n>=1)个节点，(n-1)条边的有穷集合。把它叫做“树”是因为它看起来像一个倒挂的树，也就是说它是根朝上，叶子朝下的。

3. 树结构的特点

• 树结构的每个元素称为节点（node）
• 每个节点都有零个或多个子节点
• 没有父节点的节点叫做根节点（root）
• 每一个非根结点有且只有一个父结点
• 除了根结点外，每个子结点可以分为多个不相交的子树
• 父子节点由一条有向的边（edgeo）相连结。

4. 树的常用术语

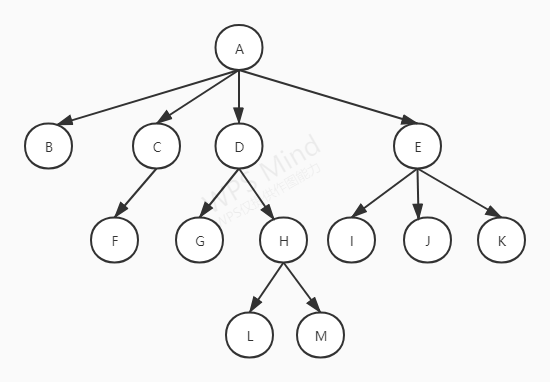
结合上图了解树的常用术语，加深对树的理解。

• 节点（node）
  树结构中的每一个元素称为一个节点，如上图中的ABC…M

• 根节点（root）
  没有父节点的节点叫做根节点，如上图中的A

• 父节点（parent）
  一个节点的上级节点叫做它的父节点，一个节点最多只能有一个父节点，如上图中C是F的父节点

• 子节点（child）
  一个节点的下级节点叫做它的子节点，一个节点的子节点可以有多个，如上图中的IJK是E的子节点

• 兄弟节点（siblings）
  拥有相同父节点的节点叫做兄弟节点，如上图中的L和M是兄弟节点

• 叶子节点（leaf）
  没有子节点的节点叫做叶子节点，如图中的BFGLMIJK

• 边（dege）
  父子节点间的连接称为边，一棵树的边数为(n-1)

• 节点的权（weight）
  节点上的元素值

• 路径（path）
  从root节点找到该节点的路线，如上图中L的路径为A-D-H-L。路径的长为该路径上边的条数，L路径的长为3（n-1）。

• 层（layer）
  距离根节点相等的路径长度为一层，如上图中A为第一层；BCDE为第二层；FGHIJK为第三层；LM为第四层

• 子树（child tree）
  以某一节点（非root）做为根的树称为子树，如以E为根的树称为A的子树

• 树的高度（height）
  树的最大层数，上图中树的高度为4

• 森林（words）
  多棵子树构成树林

5. 代码实现

我们将第3章中的树结构图通过Java代码进行实现。

TreeNode类为树的一个节点，其中：

• element：存储当前节点的元素数据
• firstChild：指向当前节点的第一个子节点（如：A的firstChild为B；D的firstChild为G；G的firstChild为空）
• nextSibling：指向当前节点的下一个兄弟节点（如：B的nextSibling为C；G的nextSibling为H；H的nextSibling为空）

Tree类实现了一棵树的初始化和遍历，listAll遍历算法的核心是递归。具体内容见代码

public class TreeDemo {

    public static void main(String[] args) {
        new Tree().initTree().listAll();

    }

    private static class Tree {

        private TreeNode root; // 树根

        /**
         * 初始化一棵树
         */
        private Tree initTree() {

            TreeNode a = new TreeNode("A");
            TreeNode b = new TreeNode("B");
            TreeNode c = new TreeNode("C");
            TreeNode d = new TreeNode("D");
            TreeNode e = new TreeNode("E");
            TreeNode f = new TreeNode("F");
            TreeNode g = new TreeNode("G");
            TreeNode h = new TreeNode("H");
            TreeNode i = new TreeNode("I");
            TreeNode j = new TreeNode("J");
            TreeNode k = new TreeNode("K");
            TreeNode l = new TreeNode("L");
            TreeNode m = new TreeNode("M");

            root = a;

            a.firstChild = b;

            b.nextSibling = c;

            c.nextSibling = d;
            c.firstChild = f;

            d.nextSibling = e;
            d.firstChild = g;

            e.firstChild = i;

            g.nextSibling = h;

            h.firstChild = l;

            i.nextSibling = j;

            j.nextSibling = k;

            l.nextSibling = m;

            return this;
        }


        /**
         * 遍历一棵树，从root开始
         */
        public void listAll() {
            listAll(root, 0);
        }

        /**
         * 遍历一棵树
         *
         * @param node  树节点
         * @param depth 层级（用于辅助输出）
         */
        public void listAll(TreeNode node, int depth) {
            StringBuilder t = new StringBuilder();
            for (int i = 0; i < depth; i++) {
                t.append("\t");
            }
            System.out.printf("%s%s\n", t.toString(), node.element);

            // 先遍历子节点，子节点的层级需要+1
            if (node.firstChild != null) {
                listAll(node.firstChild, depth + 1);
            }

            // 后遍历兄弟节点，兄弟节点的层级不变
            if (node.nextSibling != null) {
                listAll(node.nextSibling, depth);
            }
        }


    }

    private static class TreeNode {
        private final Object element; // 当前节点数据
        private TreeNode firstChild; // 当前节点的第一个子节点
        private TreeNode nextSibling; // 当前节点的下一个兄弟节点

        public TreeNode(Object element) {
            this.element = element;
        }

    }
}

输出结果：

A
	B
	C
		F
	D
		G
		H
			L
			M
	E
		I
		J
		K