本文主要是介绍C++二叉树探究，对大家解决编程问题具有一定的参考价值，需要的程序猿们随着小编来一起学习吧！

本文将对C++二叉树进行分析和代码实现。

树

定义

树（Tree）是n（n>=0)个结点的有限集。n=0时称为空树。在任意一颗非空树中：

1）有且仅有一个特定的称为根（Root）的结点；

2）当n>1时，其余结点可分为m(m>0)个互不相交的有限集T1、T2、......、Tn，其中每一个集合本身又是一棵树，并且称为根的子树。

此外，树的定义还需要强调以下两点：

1）n>0时根结点是唯一的，不可能存在多个根结点，数据结构中的树只能有一个根结点。

2）m>0时，子树的个数没有限制，但它们一定是互不相交的。

结点的度

结点拥有子树数目称为节点的度。

结点关系

结点子树的根结点为该结点的孩子结点。相应该结点称为孩子结点的双亲结点。

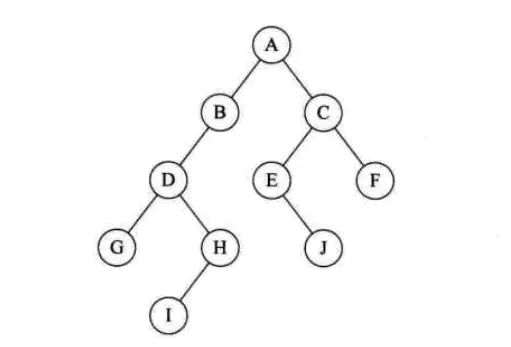
在上图中，A为B的双亲结点，B为A的孩子结点。

同一个双亲结点的孩子结点之间互称兄弟结点。

在上图中，结点B与结点C互为兄弟结点。

结点层次

从根开始定义起，根为第一层，根的孩子为第二层，以此类推。

二叉树定义

二叉树：是n（n>=0）个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成。

如下图就是一个二叉树：

二叉树特点

二叉树的特点有：

• 每个结点最多两个子树，所以二叉树中不存在度大于2的结点。注意不是只有两棵子树，而是最多有。没有子树或者有一棵子树都是可以的。
• 左子树和右子树是有顺序的，次序布恩那个任意颠倒。
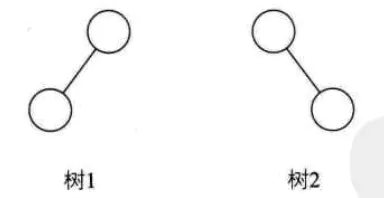
• 即使树中的某结点只有一棵子树，也要区分它是左子树还是右子树。如图：树1和树2是同一棵树，但却是不同的二叉树。

二叉树具有五种基本形态：

空二叉树；

只有一个根结点；

根结点只有左子树；

根结点只有右子树；

根结点既有左子树又有右子树。

特殊二叉树

再来介绍一些特殊的二叉树。

斜树

顾名思义，斜树一定是斜的，但是往那边斜还是有讲究的。

所有的结点都只有左子树的二叉树叫左斜树，所有结点都是只有右子树的二叉树叫右斜树。两种统称为斜树。

下面两个图分别就是左斜树和右斜树：

满二叉树

苏东坡有诗云：人有悲欢离合，月有阴晴圆缺，此事古难全。意思就是完美是理想，不完美才是人生。

我们通常看到的例子全是左高右低、参差不齐的二叉树，是否有完美的二叉树呢。

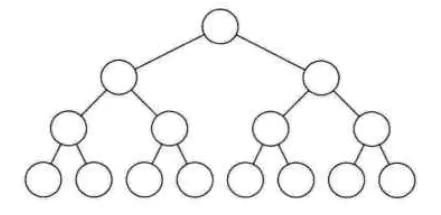
在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有的叶子结点都在同一层上，这样的二叉树叫做满二叉树。如图

单单是每个结点都有左右子树，不能算是满二叉树，还必须要所有的叶子结点都处在同一层，这样就做到了二叉树的平衡。因此满二叉树的特点有：

1. 叶子只能出现在最下面一层，出现在其他层就不能达到平衡；
2. 非叶子结点的度一定是2；
3. 同样深度的二叉树中，满二叉树的结点个数最多，叶子树最多。

完全二叉树

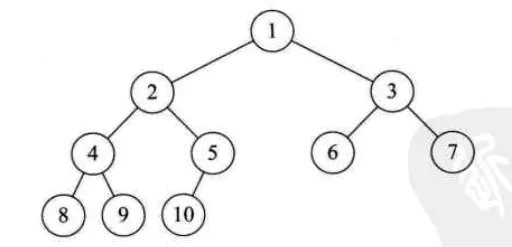
对一棵具有n个结点的二叉树按层序编号，如果编号为i（1<=i<=n）的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树。如图：

首先要从字面上区分，“完全”和“满”的差异，满二叉树一定是完全二叉树，完全二叉树不一定是满的。

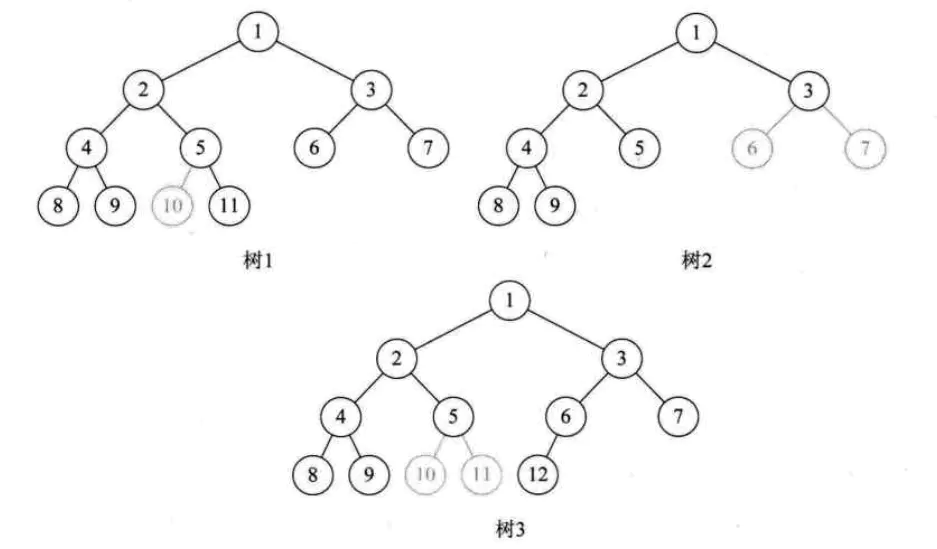
注意完全二叉树中的编号与满二叉树中的相同，而且编号全部连续，有断开的就不是完全二叉树，如下图中的三棵树都不是完全二叉树。

完全二叉树的特点：

1. 叶子结点只能出现在最下面两层；
2. 最下层的叶子一定集中在左部连续位置；
3. 倒数二层，若有叶子结点，一定都在右部连续位置；
4. 如果结点的度为1，则该结点只有左孩子，即不存在只有右子树的情况；
5. 同样结点数的二叉树，完全二叉树深度最小。

我们也得出一个判断某二叉树是否是完全二叉树的方法，那就是看着树的示意图，心中默默给每个结点按照满二叉树的结构逐层顺序编号，如果编号出现空挡，就说明不是完全二叉树，否则就是。

二叉树的性质

二叉树性质1

在二叉树的第i层上至多有2i-1个结点（i>=1）。

上图中： 第1层： 1个： 21-1=20=1 第2层： 1个： 22-1=21=2 第3层： 1个： 23-1=22=4 第4层： 8个： 24-1=23=8

通过数据归纳法，很容易得出在二叉树的第i层上最多有 2i-1个结点。

二叉树性质2

深度为k的二叉树最多有2k-1个结点（k>=1）。

这里注意是2的k次幂再减1。

如果有一层，最多1=21-1个结点 如果有两层，最多1+2=22-1个结点 如果有三层，最多1+2+4=23-1个结点 如果有四层，最多1+2+4+8=24-1个结点

通过数据归纳法的论证，可以得出如果有k层，结点数最多为2k-1。

二叉树性质3

对任何一棵二叉树T，如果其终端结点数为n0，度为2的结点数为n2，则n0=n2+1。

终端结点就是叶子结点，而一棵二叉树，除了叶子结点外，剩下的就是度为1和2的结点了，设n1是度为1的结点数。则树T的结点总数就是n=n0+n1+n2。

我们换个角度，再数一数连接线，由于根结点只有分支出去，没有分支进入，所以分支线总数为结点总数减去1，n-1=n1+2n2，又因为n=n0+n1+n2，得出n0=n2+1 。

二叉树性质4

具有n个结点的完全二叉树的深度为不大于log2n的最大整数+1 。

这里不再详细推导。

二叉树性质5

如果对一棵有n个结点的完全二叉树的结点按层序编号（从第一层到最后一层，每层从左到右），对任一结点i（1<=i<=n）有：

1. 如果i=1，则结点i是二叉树的根，无双亲；如果i>1，则其双亲是结点 ⌊ i/2 ⌋ 。
2. 如果2i>n，则结点i无左孩子（结点i为叶子结点）；否则其左孩子是结点2i 。
3. 如果2i+1>n，则结点i无右孩子；否则其右孩子是结点2i+1 。

二叉树的存储结构

顺序存储

二叉树的顺序存储结构就是使用一维数组存储二叉树中的结点，并且结点的存储位置，就是数组的下标索引。

如图所示的一棵完全二叉树采用顺序存储方式，如图表示：

由图可以看出，当二叉树为完全二叉树时，结点数刚好填满数组。
那么当二叉树不为完全二叉树时，采用顺序存储形式如何呢？例如：对于上图描述的二叉树：

其中浅色结点表示结点不存在。那么上图所示的二叉树的顺序存储结构如图所示：

其中，∧表示数组中此位置没有存储结点。此时可以发现，顺序存储结构中已经出现了空间浪费的情况。
那么对于右斜树极端情况对应的顺序存储结构如图所示：

由图可以看出，对于这种右斜树极端情况，采用顺序存储的方式是十分浪费空间的。因此，顺序存储一般适用于完全二叉树。

二叉树高度

二叉树遍历

前序遍历（根 左 右）：G D A F E M H Z

中序遍历（左 根 右）：A D E F G H M Z

后序遍历（左 右 根）：A E F D H Z M G

层次遍历（依次往下）：G D M A F H Z E

定义

二叉树的遍历是指从二叉树的根结点出发，按照某种次序依次访问二叉树中的所有结点，使得每个结点被访问一次，且仅被访问一次。
二叉树的访问次序可以分为四种：

前序遍历
中序遍历
后序遍历
层序遍历

前序遍历

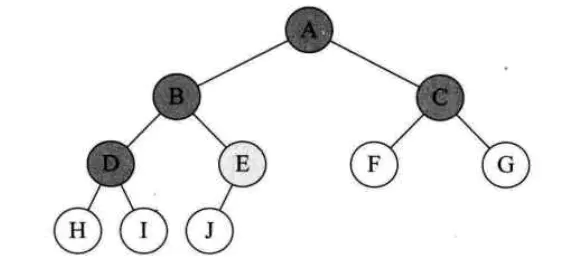
前序遍历通俗的说就是从二叉树的根结点出发，当第一次到达结点时就输出结点数据，按照先向左在向右的方向访问。

如图所示二叉树访问如下：

从根结点出发，则第一次到达结点A，故输出A;

继续向左访问，第一次访问结点B，故输出B；

按照同样规则，输出D，输出H；

当到达叶子结点H，返回到D，此时已经是第二次到达D，故不在输出D，进而向D右子树访问，D右子树不为空，则访问至I，第一次到达I，则输出I；

I为叶子结点，则返回到D，D左右子树已经访问完毕，则返回到B，进而到B右子树，第一次到达E，故输出E；

向E左子树，故输出J；

按照同样的访问规则，继续输出C、F、G；

则图所示二叉树的前序遍历输出为：
ABDHIEJCFG

中序遍历

中序遍历就是从二叉树的根结点出发，当第二次到达结点时就输出结点数据，按照先向左在向右的方向访问。

如图所示二叉树中序访问如下：

从根结点出发，则第一次到达结点A，不输出A，继续向左访问，第一次访问结点B，不输出B；继续到达D，H；

到达H，H左子树为空，则返回到H，此时第二次访问H，故输出H；

H右子树为空，则返回至D，此时第二次到达D，故输出D；

由D返回至B，第二次到达B，故输出B；

按照同样规则继续访问，输出J、E、A、F、C、G；

则如图所示二叉树的中序遍历输出为：
HDIBJEAFCG

后序遍历

后序遍历就是从二叉树的根结点出发，当第三次到达结点时就输出结点数据，按照先向左在向右的方向访问。

图3.13所示二叉树后序访问如下：

从根结点出发，则第一次到达结点A，不输出A，继续向左访问，第一次访问结点B，不输出B；继续到达D，H；
到达H，H左子树为空，则返回到H，此时第二次访问H，不输出H；

H右子树为空，则返回至H，此时第三次到达H，故输出H；

由H返回至D，第二次到达D，不输出D；

继续访问至I，I左右子树均为空，故第三次访问I时，输出I；

返回至D，此时第三次到达D，故输出D；

按照同样规则继续访问，输出J、E、B、F、G、C，A；

则图3.13所示二叉树的后序遍历输出为：
HIDJEBFGCA

虽然二叉树的遍历过程看似繁琐，但是由于二叉树是一种递归定义的结构，故采用递归方式遍历二叉树的代码十分简单。

二叉树代码实现

首先定义一个二叉树，代码如下：

	Monster m1(1,1,"刺猬");							
	Monster m2(2,2,"野狼");							
	Monster m3(3,3,"野猪");							
	Monster m4(4,4,"士兵");							
	Monster m5(5,5,"火龙");							
	Monster m6(6,6,"独角兽");							
	Monster m7(7,7,"江湖大盗");							
								
								
	TreeNode<Monster>* n1 = new TreeNode<Monster>(m1);							
	TreeNode<Monster>* n2 = new TreeNode<Monster>(m2);							
	TreeNode<Monster>* n3 = new TreeNode<Monster>(m3);							
	TreeNode<Monster>* n4 = new TreeNode<Monster>(m4);							
	TreeNode<Monster>* n5 = new TreeNode<Monster>(m5);							
	TreeNode<Monster>* n6 = new TreeNode<Monster>(m6);							
	TreeNode<Monster>* n7 = new TreeNode<Monster>(m7);							
								
	m_pRoot = n5;							
	n5->pLeft = n4;							
	n5->pRight = n6;							
	n4->pLeft = n1;							
	n1->pRight = n2;							
	n6->pLeft = n3;							
	n3->pRight = n7;							
	size = 7;

二叉树的图示如下：

这里进入反汇编跟一下二叉树的地址储存，首先找到m_pRoot的地址为3709A0

跟进去查看，发现左子树所在的地址为370938，右子树所在的地址为370A08，这里我继续跟左子树往下走

左子树所在的地址为370800，无右子树所以为000000

继续往下跟，无左子树所以为000000，右子树所在的地址为370868

继续往下跟，因为到2这个地方左子树和右子树都没有了，所以地址都为000000

这里首先实现中序遍历，这里通过上面的反汇编可以发现pName即怪物名字是在序号的8个字节之后

运行效果如下

二叉树的图示如下：

前序：5412637

中序：1245376

后序：2147365

前序实现

中序实现

后序实现

完整代码如下

// cplus二叉树.cpp : Defines the entry point for the console application.
//

#include "stdafx.h"
#include <stdio.h>
#include <Windows.h>

class Monster								
{								
public:								
	int ID;							
	int Level;							
	char Name[20];							
public:								
	Monster(){}							
	Monster(int ID,int Level,char* Name)							
	{							
		this->ID = ID;						
		this->Level = Level;						
		memcpy(&this->Name,Name,strlen(Name)+1);						
	}							
};								
								
template<class T>								
class TreeNode{								
public:								
	T element;					//当前节点存储的数据		
	TreeNode<T>* pLeft;					//指向左子节点的指针		
	TreeNode<T>* pRight;					//指向右子节点的指针		
								
	TreeNode(T& ele){							
		//初始化Node节点						
		memset(&element,0,sizeof(TreeNode));						
		//为元素赋值						
		memcpy(&element,&ele,sizeof(T));						
		pLeft = pRight = NULL;						
	}							
};								
								
template<class T>								
class BSortTree{								
public:								
	BSortTree();					//构造函数		
	~BSortTree();					//析构函数		
public:								
	void InOrderTraverse(TreeNode<T>* pNode);					//中序遍历		
	void PreOrderTraverse(TreeNode<T>* pNode);					//前序遍历		
	void PostOrderTraverse(TreeNode<T>* pNode);					//后序遍历		
	TreeNode<T>* GetRoot();					//返回根节点		
	int GetDepth(TreeNode<T>* pNode);					//返回某个节点的高度/深度		
private:								
	void Init();
	void Clear(IN TreeNode<T>* pNode);    //清理二叉树
private:								
	TreeNode<T>* m_pRoot;					//根结点指针		
	int size;					//树中元素总个数		
};								
								
template<class T> 								
BSortTree<T>::BSortTree()								
{								
	Init();							
}								
template<class T> 								
BSortTree<T>::~BSortTree()    //释放所有节点空间
{								
	printf("The destructor has been executed!\n\n");
	Clear(m_pRoot);						
								
}								
								
template<class T> 								
void BSortTree<T>::Init()								
{								
								
	Monster m1(1,1,"刺猬");							
	Monster m2(2,2,"野狼");							
	Monster m3(3,3,"野猪");							
	Monster m4(4,4,"士兵");							
	Monster m5(5,5,"火龙");							
	Monster m6(6,6,"独角兽");							
	Monster m7(7,7,"江湖大盗");							
								
								
	TreeNode<Monster>* n1 = new TreeNode<Monster>(m1);							
	TreeNode<Monster>* n2 = new TreeNode<Monster>(m2);							
	TreeNode<Monster>* n3 = new TreeNode<Monster>(m3);							
	TreeNode<Monster>* n4 = new TreeNode<Monster>(m4);							
	TreeNode<Monster>* n5 = new TreeNode<Monster>(m5);							
	TreeNode<Monster>* n6 = new TreeNode<Monster>(m6);							
	TreeNode<Monster>* n7 = new TreeNode<Monster>(m7);							
								
	m_pRoot = n5;							
	n5->pLeft = n4;							
	n5->pRight = n6;							
	n4->pLeft = n1;							
	n1->pRight = n2;							
	n6->pLeft = n3;							
	n3->pRight = n7;							
	size = 7;							
	/*							
					  5			
								
				4		    6		
								
			1		    3			
								
			     2		       7			
								
	*/							
}	

template<class T>
void BSortTree<T>::Clear(TreeNode<T>* pNode)
{
	if( pNode != NULL )
	{
		Clear(pNode->pLeft);
		Clear(pNode->pRight);
		delete pNode;
		pNode = NULL;
	}
}
							
template<class T> 								
TreeNode<T>* BSortTree<T>::GetRoot()								
{								
	return m_pRoot;							
}								
template<class T>								
int BSortTree<T>::GetDepth(TreeNode<T>* pNode)								
{								
    if(pNode==NULL) 								
    {								
	return 0;  							
    }								
    else  								
    {  								
        int m = GetDepth(pNode->pLeft);  								
        int n = GetDepth(pNode->pRight);  								
        return (m > n) ? (m+1) : (n+1);   								
    }  								
}								
template<class T> 								
void BSortTree<T>::InOrderTraverse(TreeNode<T>* pNode)    //中序遍历所有怪物,列出怪的名字(左 根 右)							
{
	char* pName = NULL;

	if (pNode != NULL)
	{
		InOrderTraverse(pNode->pLeft);
		pName = (char*)&pNode->element;
		pName = pName + 8; 

		printf("Use InOrderTraverse,the value is:%d\n",pNode->element);
		printf("Use InOrderTraverse,the name is:%s\n",pName);

		InOrderTraverse(pNode->pRight);
	}
														
}								
								
template<class T> 								
void BSortTree<T>::PreOrderTraverse(TreeNode<T>* pNode)    //前序遍历所有怪物,列出怪的名字(根 左 右)						
{	
	char* pName = NULL;

	if (pNode != NULL)
	{
		pName = (char*)&pNode->element;
		pName = pName + 8; 

		printf("Use PreOrderTraverse,the value is:%d\n",pNode->element);
		printf("Use PreOrderTraverse,the name is:%s\n",pName);

		PreOrderTraverse(pNode->pLeft);
		PreOrderTraverse(pNode->pRight);
	}
								
								
}								
								
template<class T> 								
void BSortTree<T>::PostOrderTraverse(TreeNode<T>* pNode)    //后序遍历所有怪物,列出怪的名字(左 右 根)								
{	
	char* pName = NULL;

	if (pNode != NULL)
	{
		pName = (char*)&pNode->element;
		pName = pName + 8; 

		PreOrderTraverse(pNode->pLeft);
		PreOrderTraverse(pNode->pRight);

		printf("Use PostOrderTraverse,the value is:%d\n",pNode->element);
		printf("Use PostOrderTraverse,the name is:%s\n",pName);
	}
								
								
}								
								

void TestSecondtree()
{
	
	BSortTree<Monster>* p = new BSortTree<Monster>;
	
	p->InOrderTraverse(p->GetRoot());

	p->PreOrderTraverse(p->GetRoot());

    p->PostOrderTraverse(p->GetRoot());
	
    delete p;
	

	
}

int main(int argc, char* argv[])
{
	TestSecondtree();

	return 0;
}

搜索二叉树/二叉排序树

搜索二叉树/二叉排序树的特点：

1、有很好的查询性能

2、有很好的新增和删除的性能

3、若左子树不空，则左子树上所有结点的值均小于它的根结点的值

4、若右子树不空，则右子树上所有结点的值均大于它的根结点的值

5、左、右子树也分别为二叉排序树

中序遍历就能够直接从小到大排列：3 5 6 7 10 12 13 15 16 18 20 23

搜索二叉树的删除

情况1：叶子节点

1、删除该节点

2、将父节点(左或者右)指针置NULL

情况2：只有一个子树

1、删除该节点

2、将父节点(左或者右)指针指向子树

情况3：左右子树都有

1、用右子树最小的节点取代源节点

2、再递归删除最小节点

搜索二叉树代码实现

首先测试一下输出情况，no problem

完整代码如下主要是遍历的思想

// cplus搜索二叉树.cpp : Defines the entry point for the console application.
//

#include "stdafx.h"
#include <stdio.h>
#include <Windows.h>

#define SUCCESS           1 // 执行成功			
#define ERROR			 -1 // 执行失败			         
						
template<class T>						
class TreeNode{						
public:						
	T element;					//当前节点存储的数据
	TreeNode<T>* pLeft;					//指向左子节点的指针
	TreeNode<T>* pRight;					//指向右子节点的指针
	TreeNode<T>* pParent;					//指向父结点的指针
						
						
	TreeNode(T& ele){					
		//初始化Node节点				
		memset(&element,0,sizeof(TreeNode));				
		//为元素赋值				
		memcpy(&element,&ele,sizeof(T));				
		pLeft = pRight = pParent = NULL;				
	}					
	//重载== 比较两结点是否相等					
	bool operator==(TreeNode<T>* node){ 					
		return node->element == element ? true : false;				
	}					
};						
						
template<class T>						
class BSortTree{						
public:						
	BSortTree();					
	~BSortTree();					
public:						
	bool IsEmpty();					
	DWORD Insert(T element);					
	void Delete(T element);					
	TreeNode<T>* Search(T element);					
	void InOrderTraverse(TreeNode<T>* pNode);					
	void PreOrderTraverse(TreeNode<T>* pNode);					
	void PostOrderTraverse(TreeNode<T>* pNode);					
private:						
	TreeNode<T>* GetMaxNode(TreeNode<T>* pNode);					
	TreeNode<T>* GetMinNode(TreeNode<T>* pNode);					
	TreeNode<T>* SearchNode(TreeNode<T>* pNode,T element);					
	DWORD InsertNode(T element, TreeNode<T>* pNode);					
	TreeNode<T>* DeleteNode(T element, TreeNode<T>* pNode);					
	void Clear(TreeNode<T>* pNode);					
private:						
	TreeNode<T>* m_pRoot;					
	int size;					
};						
						
template<class T> 						
BSortTree<T>::BSortTree()						
{						
	m_pRoot = NULL;					
	size = 0;					
}						
template<class T> 						
BSortTree<T>::~BSortTree(){						
						
	Clear(m_pRoot);					
}						
template<class T> 						
DWORD BSortTree<T>::Insert(T element)						
{						
	//如果根节点为空					
	if ( !m_pRoot )					
	{					
		m_pRoot = new TreeNode<T>(element);				
		size++;				
		return SUCCESS;				
	}					
	//如果根节点不为空					
	return InsertNode(element, m_pRoot);					
}						
template<class T> 						
DWORD BSortTree<T>::InsertNode(T element, TreeNode<T>* pNode)						
{						
	//将元素封装到节点中					
	TreeNode<T>* pNewNode = new TreeNode<T>(element);
	
	//如果element == 当前节点 直接返回					
	if(element == pNode->element)					
	{					
		return SUCCESS;				
	}				
	
	//如果pNode的左子节点为NULL 并且element < 当前节点					
	if(pNode->pLeft == NULL && element < pNode->element)					
	{					
		pNode->pLeft = pNewNode;				
		pNewNode->pParent = pNode;				
		size++;				
		return SUCCESS;				
	}	
				
	//如果pNode的右子节点为NULL 并且element > 当前节点					
	if(pNode->pRight == NULL && element > pNode->element){					
		pNode->pRight = pNewNode;				
		pNewNode->pParent = pNode;				
		size++;				
		return SUCCESS;				
	}					
	//如果element<当前节点 且当前节点的左子树不为空					
	if(element < pNode->element)					
	{					
		InsertNode(element,pNode->pLeft);				
	}					
	else					
	{					
		InsertNode(element,pNode->pRight);				
	}					
	return SUCCESS;					
}						
						
template<class T> 						
void BSortTree<T>::Clear(TreeNode<T>* pNode)						
{						
	if(pNode!=NULL)					
	{					
		Clear(pNode->pLeft);				
		Clear(pNode->pRight);				
		delete pNode;				
		pNode=NULL;				
	}					
}						
						
template<class T> 						
bool BSortTree<T>::IsEmpty()						
{						
	return size==0 ? true : false;					
}						
						
template<class T> 						
TreeNode<T>* BSortTree<T>::Search(T element)						
{						
	return SearchNode(m_pRoot, element);					
}						
template<class T> 						
TreeNode<T>* BSortTree<T>::SearchNode(TreeNode<T>* pNode,T element)						
{						
	if(pNode == NULL)					//如果节点为NULL
	{					
		return NULL;				
	}					
	else if(element == pNode->element)					//如果相等
	{					
		return pNode;				
	}					
	else if(element < pNode->element)		//如果比节点的元素小 向左找			
	{					
		return SearchNode(pNode->pLeft,element);				
	}					
	else					//如果比节点的元素大 向右找
	{					
		return SearchNode(pNode->pRight,element);				
	}					
}						
						
template<class T> 						
void BSortTree<T>::Delete(T element)						
{						
	if (! m_pRoot == NULL)	//指针为空则二叉树没有成员
	{
		printf("No member is in the binary tree and cannot be deleted!\n");
	}
	else  //调用DeleteNode()方法删除节点
	{
		TreeNode<T>* ptemp = SearchNode(m_pRoot , element);
		DeleteNode(element, ptemp);
	}
	
}						
						
template<class T> 						
TreeNode<T>* BSortTree<T>::DeleteNode(T element,TreeNode<T>* pNode)						
{						
						
	if (!pNode->pLeft && !pNode->pRight)	//无左子树也无右子树
	{
		if (pNode->element < pNode->pParent->element)
		{
			pNode->pParent->pLeft = NULL;
		}
		else
		{
			pNode->pParent->pRight = NULL;
		}
		delete pNode;
	}
	
	else if (pNode->pLeft && !pNode->pRight)	//有左子树无右子树
	{
		if (pNode->element < pNode->pParent->element)
		{
			pNode->pParent->pLeft = pNode->pLeft;
			pNode->pLeft->pParent = pNode->pParent;
		}
		else
		{
			pNode->pParent->pRight = pNode->pLeft;
			pNode->pLeft->pParent = pNode->pParent;
		}
		delete pNode;
	}

	else if (!pNode->pLeft && pNode->pRight)	//无左子树有右子树
	{
		if (pNode->elment < pNode->pParent->element)
		{
			pNode->pParent->pLeft = pNode->pRight;
			pNode->pRight->pParent = pNode->pParent;
		}
		else
		{
			pNode->pParent->pRight = pNode->p Right;
			pNode->pRight->pParent = pNode->pParent;
		}
		delete pNode;
	}
	else (pNode->pLeft && pNode->pRight)	//左右子树都有
	{
		TreeNode<T>* pRightMinNode = GetRightMinNode(pNode->pRight);
		pNode->element = pRightMinNode->element;
		DeleteNode(pRightMinNode->element, pRightMinNode);
		
	}

	return NULL;					
}						
												
						
						
//测试代码：						
						
						
void TestInsert()						
{						
	//12 8 5 9 17 15 13					
	/*					
				12		
						
		8				17
						
	5		9		15	
						
				13		
						
	*/					
						
	BSortTree<int> tree;					
						
	tree.Insert(12);					
	tree.Insert(8);					
	tree.Insert(5);					
	tree.Insert(9);					
	tree.Insert(17);					
	tree.Insert(15);					
	tree.Insert(13);					
}						
						
void TestSearch()						
{						
	//12 8 5 9 17 15 13					
						
	BSortTree<int> tree;					
						
	tree.Insert(12);					
	tree.Insert(8);					
	tree.Insert(5);					
	tree.Insert(9);					
	tree.Insert(17);					
	tree.Insert(15);					
	tree.Insert(13);					
						
	TreeNode<int>* p = tree.Search(9);
	TreeNode<int>* q = tree.Search(17);			
						
	printf("The search value is:%d\nThe address of search value is:%x\n",p->element,p);	
	printf("The search value is:%d\nThe address of search value is:%x\n",q->element,q);				
}	


int main(int argc, char* argv[])
{
	TestInsert();
	TestSearch();

	return 0;
}

这篇关于C++二叉树探究的文章就介绍到这儿，希望我们推荐的文章对大家有所帮助，也希望大家多多支持为之网！