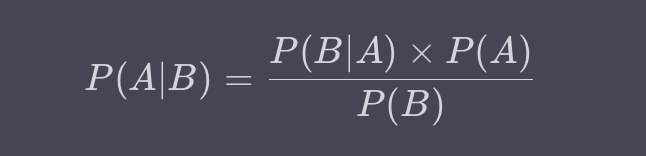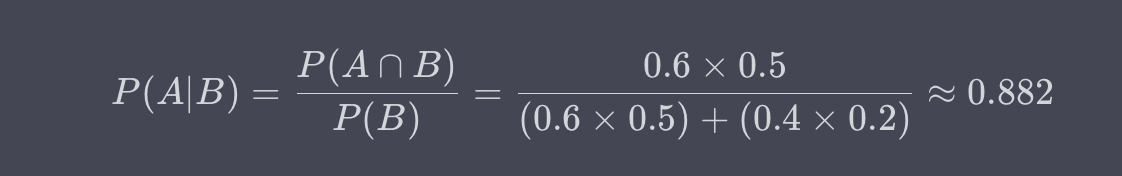朴素贝叶斯深度解码:从原理到深度学习应用
2023/11/18 21:07:18
本文主要是介绍朴素贝叶斯深度解码:从原理到深度学习应用,对大家解决编程问题具有一定的参考价值,需要的程序猿们随着小编来一起学习吧!
本文深入探讨了朴素贝叶斯算法,从基础的贝叶斯定理到算法的各种变体,以及在深度学习和文本分类中的应用。通过实战演示和详细的代码示例,展示了朴素贝叶斯在自然语言处理等任务中的实用性和高效性。
一、简介
朴素贝叶斯(Naive Bayes)是一种基于贝叶斯定理的分类技术,具有实现简单、易于理解、且在多种应用场景中表现优秀的特点。本节旨在介绍贝叶斯定理的基本历史和重要性,以及朴素贝叶斯分类器的应用场景。
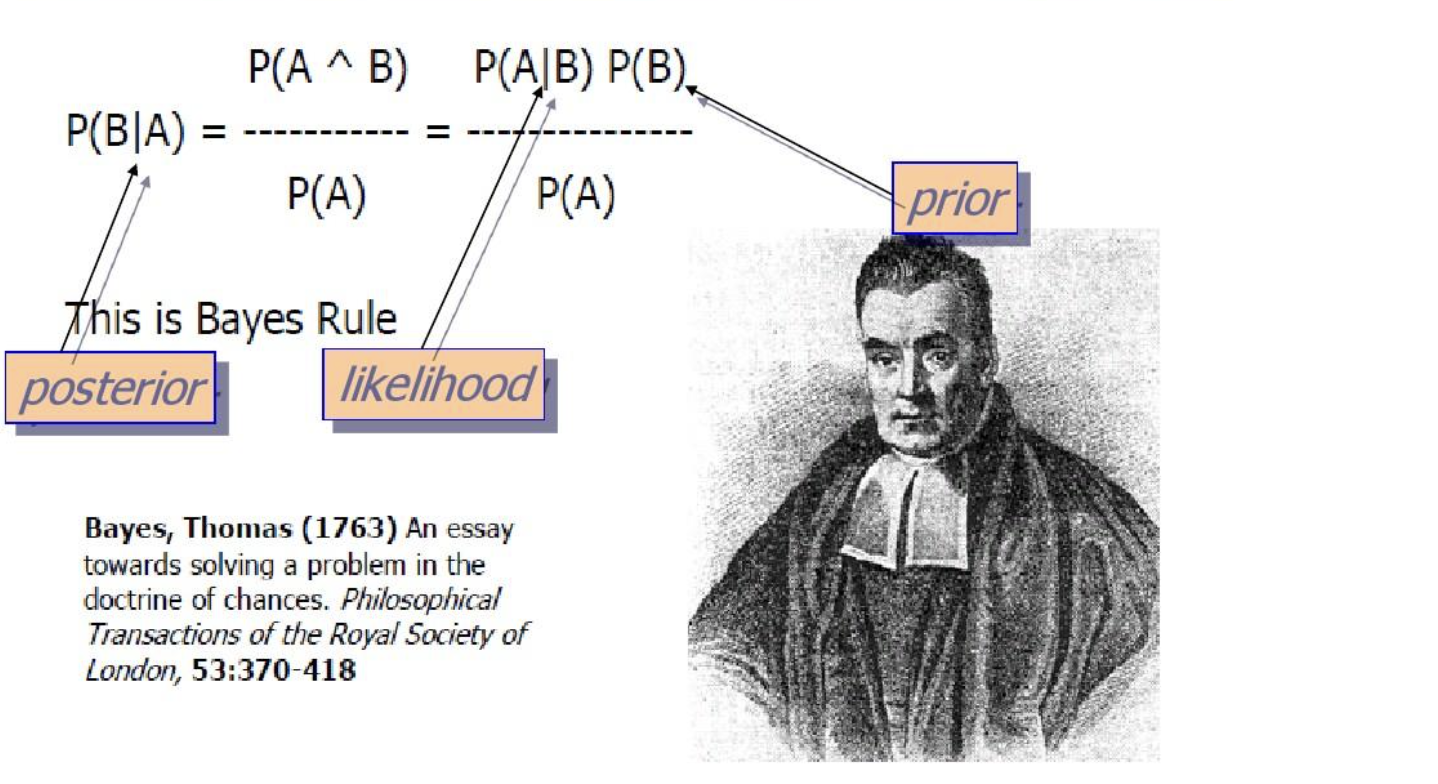
贝叶斯定理的历史和重要性
定义
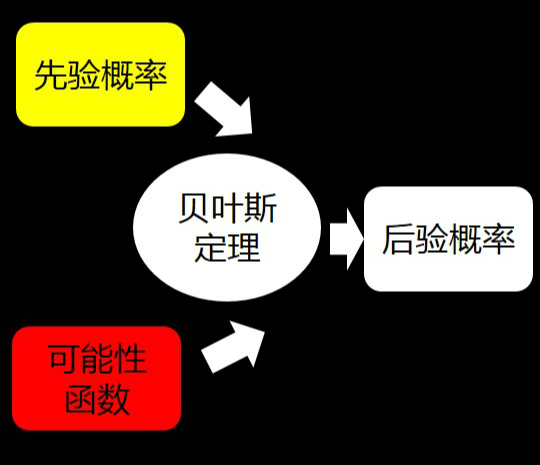
**贝叶斯定理(Bayes’ Theorem)**是一种在已知某个条件下,预测另一个条件概率的方法。数学表达式为:
例子
比如,在医学检测中,已知某种疾病在总体中的发病率P(A),以及某项检测的准确率P(B|A),贝叶斯定理就能用于预测某个检测结果阳性的人实际患病的概率P(A|B)。
朴素贝叶斯分类器的应用场景
定义
**朴素贝叶斯分类器(Naive Bayes Classifier)**是一种应用贝叶斯定理,以及一个“朴素”的假设,即特征间相互独立,来进行分类的算法。
例子
垃圾邮件过滤就是朴素贝叶斯分类器的一个经典应用。通过学习垃圾邮件和非垃圾邮件中词汇的出现频率,朴素贝叶斯分类器能够预测一个新邮件是否为垃圾邮件。
常见应用场景
- 文本分类:除了垃圾邮件过滤,还广泛应用于新闻分类、情感分析等。
- 推荐系统:例如,根据用户以往的购买历史和浏览记录,预测用户可能感兴趣的其他产品。
- 医学诊断:如基于病人的一系列检测结果,预测病人是否患有某种疾病。
二、贝叶斯定理基础
贝叶斯定理是一种数学工具,用于在给定某些观察或数据的情况下,计算不同事件的条件概率。本节将详细介绍与贝叶斯定理相关的几个基本概念:条件概率、贝叶斯公式,以及它们在现实世界中的应用示例。
条件概率
定义
**条件概率(Conditional Probability)**是在给定某一事件B发生的条件下,另一事件A发生的概率。数学上,条件概率用P(A|B)表示,计算公式为:
例子
假设一个课堂里有60%的男生和40%的女生。其中,50%的男生和20%的女生喜欢数学。现在,如果随机选一个喜欢数学的学生,那么这个学生是男生的条件概率是多少?
解:这里,A是学生是男生,B是学生喜欢数学。需要找的是P(A|B),即给定一个学生喜欢数学,在这个条件下,这个学生是男生的概率。
因此,给定一个喜欢数学的学生,这个学生是男生的条件概率约为0.882或88.2%。
贝叶斯公式
定义
**贝叶斯公式(Bayes’ Formula)**是一个用于更新随机事件概率估计的公式。基础形式为:
例子
在医学检测中,假设某疾病在总人口中的患病率P(A) 为1%。某项检测对这种疾病的诊断准确率P(B|A) 为99%。现在,这项检测的结果对一个人是阳性,求这个人实际上患有这种疾病的概率P(A|B) 。
三、朴素贝叶斯算法原理
朴素贝叶斯(Naive Bayes)算法是一种基于贝叶斯定理的分类算法,其“朴素”之处在于假设所有特征都是互相独立的。本节将深入探讨该算法的基本构成、分类过程、以及不同变体。
基本构成
定义
朴素贝叶斯分类器用以下公式描述分类过程:
例子
假设我们有一个天气预测模型,用于预测明天是晴天(Sunny)还是多云(Cloudy)。我们的特征有两个:温度(高、低)和湿度(高、低)。假设先验概率P(Sunny)=0.6,P(Cloudy)=0.4,以及一些已知的条件概率(例如,P(高温 | Sunny) = 0.7等)。
现在,给定一个具有“高温”和“低湿度”的天气情况,我们可以使用朴素贝叶斯公式来计算明天是晴天还是多云的概率。
分类过程
定义
朴素贝叶斯算法通常包含以下步骤:
- 计算先验概率:基于训练数据集,计算每个类别Ck的先验概率P(Ck)。
- 计算条件概率:对于每个特征xi和每个类别Ck,计算P(xi | Ck)。
- 应用贝叶斯公式:对于一个新的样本,应用贝叶斯公式来计算所有可能类别的后验概率。
- 分类决策:选择具有最高后验概率的类别作为样本的预测分类。
例子
继续上面的天气预测模型,假设我们已经从历史数据中计算出了各种先验概率和条件概率。现在,对于一个具有“高温”和“低湿度”的新样本,我们将:
- 计算该样本属于“晴天”和“多云”的后验概率。
- 比较两个后验概率,并选择概率更高的类别作为预测结果。
不同变体
定义
根据特征的不同类型(连续或离散)和分布(高斯、多项式等),朴素贝叶斯算法有几个不同的变体:
- 高斯朴素贝叶斯(Gaussian Naive Bayes):用于连续特征,假设特征服从高斯分布。
- 多项式朴素贝叶斯(Multinomial Naive Bayes):常用于文本分类,特征表示词频。
- 伯努利朴素贝叶斯(Bernoulli Naive Bayes):用于二值特征。
例子
- 高斯朴素贝叶斯:在垃圾邮件分类中,如果特征是每封邮件的长度和使用某些关键词的频率,我们可能会使用高斯朴素贝叶斯。
- 多项式朴素贝叶斯:在文本分类中,比如新闻文章分为政治、体育、娱乐等,通常使用多项式朴素贝叶斯。
- 伯努利朴素贝叶斯:在情感分析中,如果我们只关心某个词是否出现(而不是出现的次数),则可能会使用伯努利朴素贝叶斯。
四、朴素贝叶斯的种类
朴素贝叶斯算法有多种变体,每种都有其特定的应用场景和假设。本节将详细探讨这些不同类型的朴素贝叶斯分类器。
高斯朴素贝叶斯(Gaussian Naive Bayes)
定义
高斯朴素贝叶斯是最常用于连续特征的朴素贝叶斯分类器。该模型假设每个类别中每个特征的值都服从高斯(正态)分布。
例子
考虑一个简单的肿瘤分类问题,特征是肿瘤的大小和年龄。我们可以通过高斯朴素贝叶斯模型来预测一个新样本(例如,大小为2.5cm、年龄45岁)是良性或恶性的。
多项式朴素贝叶斯(Multinomial Naive Bayes)
定义
多项式朴素贝叶斯通常用于离散特征,特别是在文本分类问题中。该模型假设特征是由一个简单多项式分布生成的。
例子
在新闻分类中,假设我们有三个类别:政治、科技和娱乐。特征则是每篇文章中单词的频数。多项式朴素贝叶斯可以有效地预测一个新文章的类别。
伯努利朴素贝叶斯(Bernoulli Naive Bayes)
定义
伯努利朴素贝叶斯适用于二值特征模型。与多项式朴素贝叶斯不同,这种模型只考虑特征是否出现。
例子
在情感分析中,特征可能是某些情感词(如“好”或“坏”)是否出现在文本中。伯努利朴素贝叶斯可以用于预测文本(例如,产品评论)是正面还是负面。
五、朴素贝叶斯在深度学习中的应用
朴素贝叶斯(Naive Bayes)和深度学习都是机器学习的重要分支,但它们在许多方面都有根本的不同。然而,这并不意味着两者不能结合使用。本节将探讨朴素贝叶斯在深度学习领域中的具体应用。
数据预处理和特征选择
定义
在深度学习模型训练之前,朴素贝叶斯算法可以用于数据预处理和特征选择。它能快速地评估特征与标签之间的相关性,为复杂的深度学习模型提供有用的信息。
例子
例如,在图像分类任务中,我们可以先用朴素贝叶斯对像素级特征进行预筛选,识别哪些特征与目标类别最相关,然后只用这些特征去训练卷积神经网络(CNN)模型。
生成对抗网络(GANs)中的生成模型
定义
在生成对抗网络(GANs)中,朴素贝叶斯可以作为一个简单的生成模型与判别模型配合使用。尽管它没有深度生成模型那么强大,但在一些场景下,它足够生成合理的数据分布。
例子
假设我们正在尝试生成文本数据。一般来说,LSTM或Transformer更常用于这类问题,但在某些特定应用中,朴素贝叶斯足够生成简单的文本数据,例如垃圾邮件生成等。
作为基线模型
定义
朴素贝叶斯由于其简单和计算高效的特点,经常被用作深度学习任务的基线模型。这能提供一个基准,让研究人员更容易评估深度学习模型的性能是否有显著提升。
例子
在自然语言处理(NLP)任务,比如情感分类上,朴素贝叶斯往往是一个很好的起点。如果一个复杂的深度学习模型(如BERT)与朴素贝叶斯有相似的性能,这通常意味着深度学习模型需要进一步优化。
异常检测与解释性
定义
深度学习模型通常作为黑箱操作,而朴素贝叶斯由于其概率基础,可以用于解释深度学习模型的决策过程,特别是在异常检测场景下。
例子
在信用卡欺诈检测系统中,一个深度学习模型可能很好地识别出异常行为,但朴素贝叶斯可以进一步提供哪些特征最可能导致该行为被标记为异常,从而提供更多的解释性。
六、实战:文本分类
在这一节中,我们将通过一个具体的例子来实战演示如何使用朴素贝叶斯进行文本分类。文本分类是NLP(自然语言处理)中一个非常基础和广泛应用的任务,通常用于垃圾邮件检测、情感分析、主题分类等。
任务定义
定义
文本分类的目标是自动将文本内容分到预定义的类别。例如,在情感分析中,预定义的类别可能是积极、消极和中性。
例子
一个典型的应用场景是电影评论的情感分析。给定一段电影评论文本,目标是判断这段评论是正面的、负面的,还是中性的。
数据预处理
定义
数据预处理通常包括去除停用词、词干提取、分词等。
例子
例如,句子 “This movie is not good” 经过预处理后可能变为 ['movie', 'not', 'good']。
朴素贝叶斯分类器训练
下面的代码段是用Python和scikit-learn库进行朴素贝叶斯分类器训练的完整实例。
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 示例数据集
X = ["I love this movie", "I hate this movie", "Not bad", "Not good"]
y = ["Positive", "Negative", "Neutral", "Neutral"]
# 数据预处理(向量化)
vectorizer = CountVectorizer()
X_vec = vectorizer.fit_transform(X)
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X_vec, y, test_size=0.25, random_state=42)
# 训练朴素贝叶斯分类器
clf = MultinomialNB()
clf.fit(X_train, y_train)
# 测试模型
y_pred = clf.predict(X_test)
# 输出准确度
print("Accuracy:", accuracy_score(y_test, y_pred))
输入和输出
- 输入:一组标记(Positive, Negative, Neutral)的文本数据。
- 输出:模型对测试集的分类准确度。
处理过程
- 使用
CountVectorizer将文本数据转换为向量。 - 使用
train_test_split将数据集划分为训练集和测试集。 - 使用
MultinomialNB(多项式朴素贝叶斯)进行模型训练。 - 使用训练好的模型对测试集进行预测。
- 使用
accuracy_score计算模型准确度。
七、总结
朴素贝叶斯算法是一个简单但强大的工具,不仅在传统机器学习领域有广泛应用,还能与深度学习算法相辅相成。从基础的贝叶斯定理到算法的多种变体,再到深度学习中的具体应用场景,朴素贝叶斯展示了其独特的优点和潜力。
独特洞见
-
互补性与简单性:朴素贝叶斯和深度学习在许多方面都是互补的。当深度学习模型因其复杂性而难以解释时,朴素贝叶斯能够提供更多的可解释性。
-
速度与效率:朴素贝叶斯因其算法简单和计算高效,非常适用于数据预处理和特征选择,这在深度学习任务中尤为重要。
-
自然语言处理中的广泛应用:通过实战演示,我们了解到朴素贝叶斯在文本分类方面具有不小的潜力,尤其是当数据稀疏或标签非常不平衡时。
-
模型解释与信任度:在现实世界的应用场景,比如医疗诊断或金融风险评估中,模型的解释性往往与准确性同等重要。朴素贝叶斯能够提供这一点,而深度学习则往往缺乏这方面的能力。
-
模型融合与集成学习:朴素贝叶斯由于其计算简单和预测速度快,常常作为集成学习方法中的一部分,与其他更复杂的模型组合,以达到更高的准确度。
综上所述,朴素贝叶斯是一个不容忽视的算法。在当前由深度学习主导的人工智能领域里,朴素贝叶斯仍然占有一席之地。正因为其简单、高效和易于解释,这使得它成为了各种机器学习任务,尤其是自然语言处理和数据预处理中的重要工具。通过深入地掌握和理解这一算法,我们可以更全面地认识到机器学习的多样性和灵活性,这对于任何希望深入了解这一领域的人来说,都是极其宝贵的。
这篇关于朴素贝叶斯深度解码:从原理到深度学习应用的文章就介绍到这儿,希望我们推荐的文章对大家有所帮助,也希望大家多多支持为之网!
- 2024-12-24酒店香薰厂家:创造独特客户体验
- 2024-12-22程序员出海做 AI 工具:如何用 similarweb 找到最佳流量渠道?
- 2024-12-20自建AI入门:生成模型介绍——GAN和VAE浅析
- 2024-12-20游戏引擎的进化史——从手工编码到超真实画面和人工智能
- 2024-12-20利用大型语言模型构建文本中的知识图谱:从文本到结构化数据的转换指南
- 2024-12-20揭秘百年人工智能:从深度学习到可解释AI
- 2024-12-20复杂RAG(检索增强生成)的入门介绍
- 2024-12-20基于大型语言模型的积木堆叠任务研究
- 2024-12-20从原型到生产:提升大型语言模型准确性的实战经验
- 2024-12-20啥是大模型1