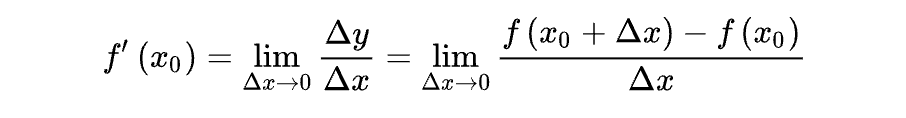梯度下降，原来如此？

写在最前

这个故事比较适合对机器学习训练过程有些许了解的同学。当然啦，即使你还没有踏入机器学习的世界，也是可以来瞧一瞧的，因为“梯度下降”这个知识点相对独立。即使只是来“瞟一眼”，也能收获不少印象的

后续我还会带来一个关于机器学习训练过程的故事，这次就先当做是提前热热身吧！

在这个 AI 内容生成泛滥的时代，依然有一批人"傻傻"坚持原创，如果您能读到最后，还请点赞或收藏或关注支持下我呗，感谢 (￣︶￣)↗

解决什么问题？

蛋先生：嘿，丹尼尔，走路专心点，想啥呢？

丹尼尔：没啥，就是最近看了一点关于机器学习的东西，尤其是梯度下降，感觉有点懂又不完全懂。既然遇到你了，聊聊吧？

蛋先生：（咳咳，清了清嗓子）~

丹尼尔：我想听听你对梯度下降的理解

蛋先生：我可没说我懂哦

丹尼尔：哎呀，你肯定是“略懂”啊，这点我知道 (^▽ )

蛋先生：你小子 (lll￢ω￢)。那我问你啊，梯度下降在机器学习里究竟是为了什么呢？

丹尼尔：不就是为了找到某个损失函数的最小值，从而确定模型的最佳参数嘛。损失函数的值越小，训练时模型预测的输出值与实际值的误差就越小

蛋先生：嗯，功课做得不错啊。你这不是已经懂了嘛

丹尼尔：No，我只是知其然而不知其所以然。为啥梯度下降就能找到最小值呢？

蛋先生：为了找到最小值，我们需要不断调整参数，使得模型输出值与实际值越来越接近。那么每次参数应该调整多少，往哪个方向调整？这，就是梯度下降要解决的问题了

梯度下降和导数

丹尼尔：要不，你还是先让我有点画面感吧

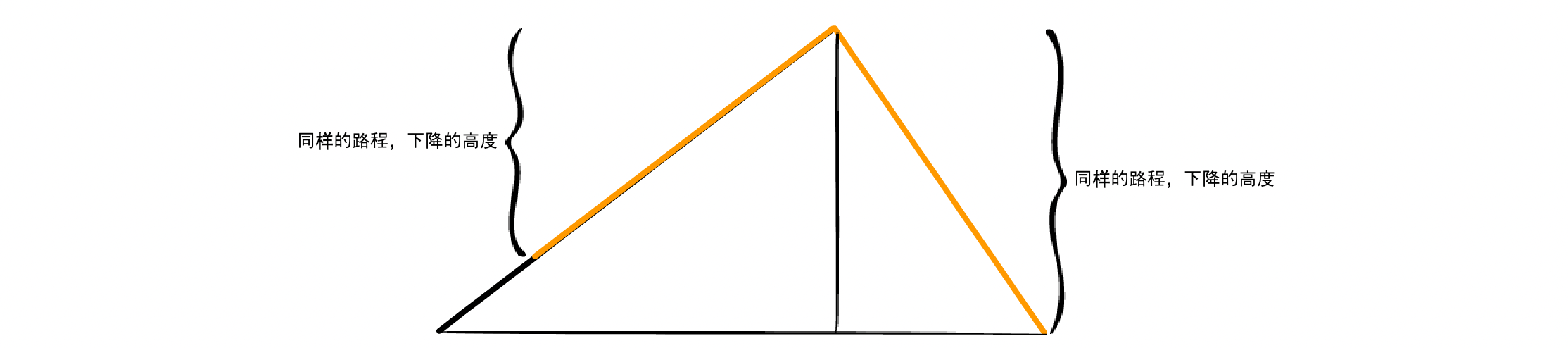
蛋先生：好啊，梯度下降这个名字本身就很形象了。想象你站在山顶，想要最快地到达山脚。你会选择朝最陡峭的方向下山，因为最陡峭的方向意味着在相同的距离内下降的高度最多，因此所需的时间最短

丹尼尔：嗯，有点画面了。咱们可以回到刚刚那个问题了，梯度下降到底是什么？为什么它能指明参数调整的大小和方向呢？

蛋先生：这就不得不提到导数了。梯度其实就是损失函数对各个参数的偏导数的集合（向量）

梯度 = [参数1的偏导数, 参数2的偏导数, ...]

丹尼尔：导数？偏导数？有点晕了~

蛋先生：简单来说，导数是针对只有一个自变量（参数）的函数而言的，而我们的情况涉及多个参数。在计算每个参数的导数时，我们固定其它参数的值，这个导数就称为偏导数（偏向于那个参数的导数）。但我们要调整的是一组参数，所以梯度就是这些偏导数的集合

丹尼尔：哦，也就是说，梯度的核心是导数。那么问题来了，导数为什么能指明参数调整的大小和方向呢？

导数的意义

蛋先生：先来简单了解一下导数。导数描述的是函数在某一点的瞬时变化率，反映了函数值随自变量（这里指参数）变化的快慢和方向

丹尼尔：某一点的瞬时变化率？怎么理解呢？

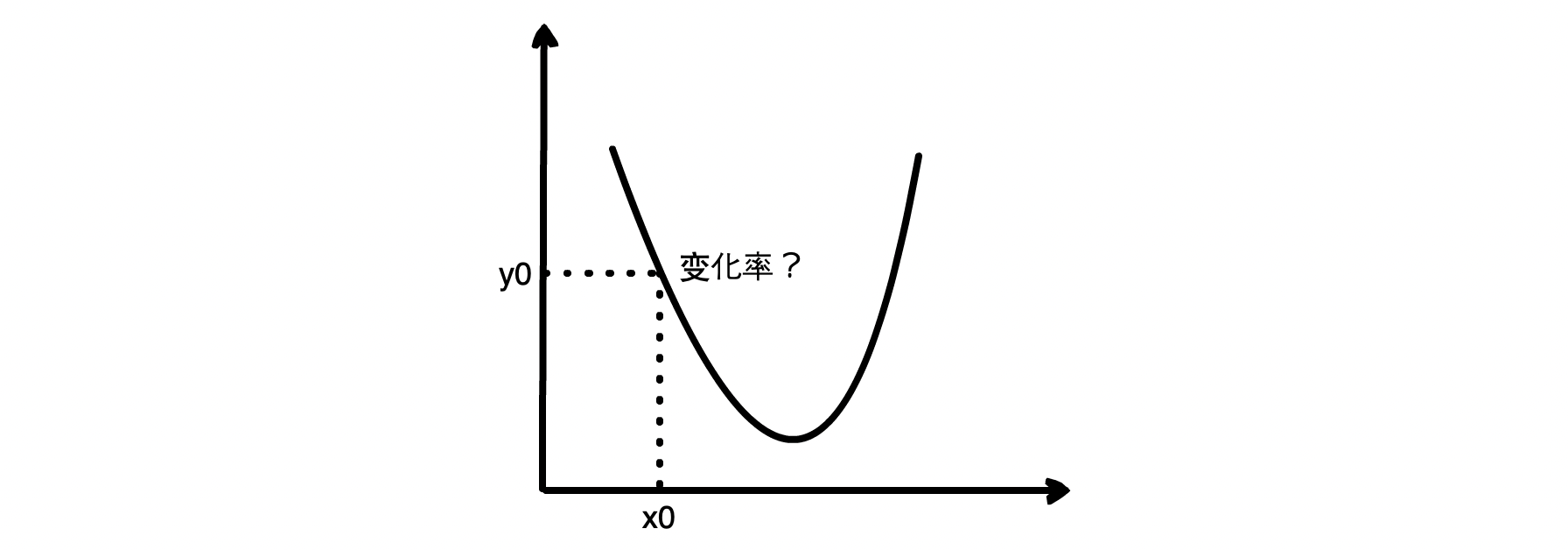
蛋先生：我们先来看一个函数 y = f(x)。某一点的瞬时变化率就是当 x 取特定值 x0 时，y 相对于 x 的变化快慢情况，也就是瞬时变化率，称为导数，可以用符号 f’(x0) 或 df(x0)/dx 表示

丹尼尔：慢着，当 x 等于 x0 时，我只知道 y 的值为 y0，那如何求得 y 的瞬时变化率呢？

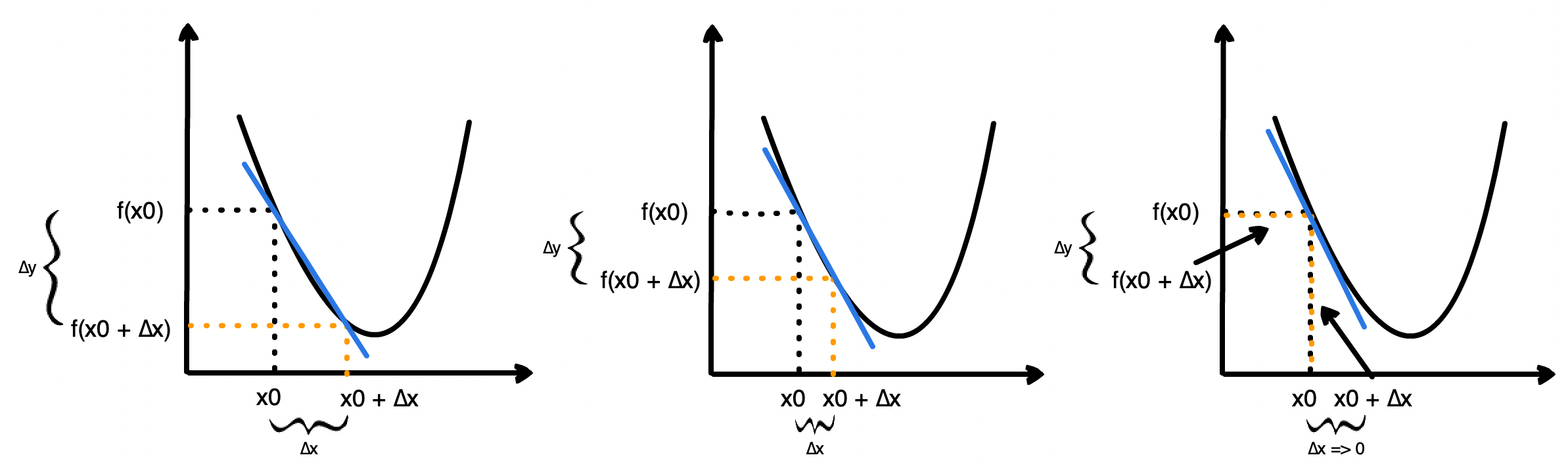
蛋先生：假设 x 从 x0 增加到 x + ∆x ，增量为 ∆x，而对应的 y 从 f(x0) 变成 f(x0 + ∆x)，增量记为 ∆y，那么此时 y 相对于 x 的平均变化率就是 ∆y/∆x。如果我们让 ∆x 趋近于 0，就可以得到 x0 点附近 y 相对于 x 的瞬时变化率

丹尼尔：哦，那这个瞬时变化率有什么意义呢？

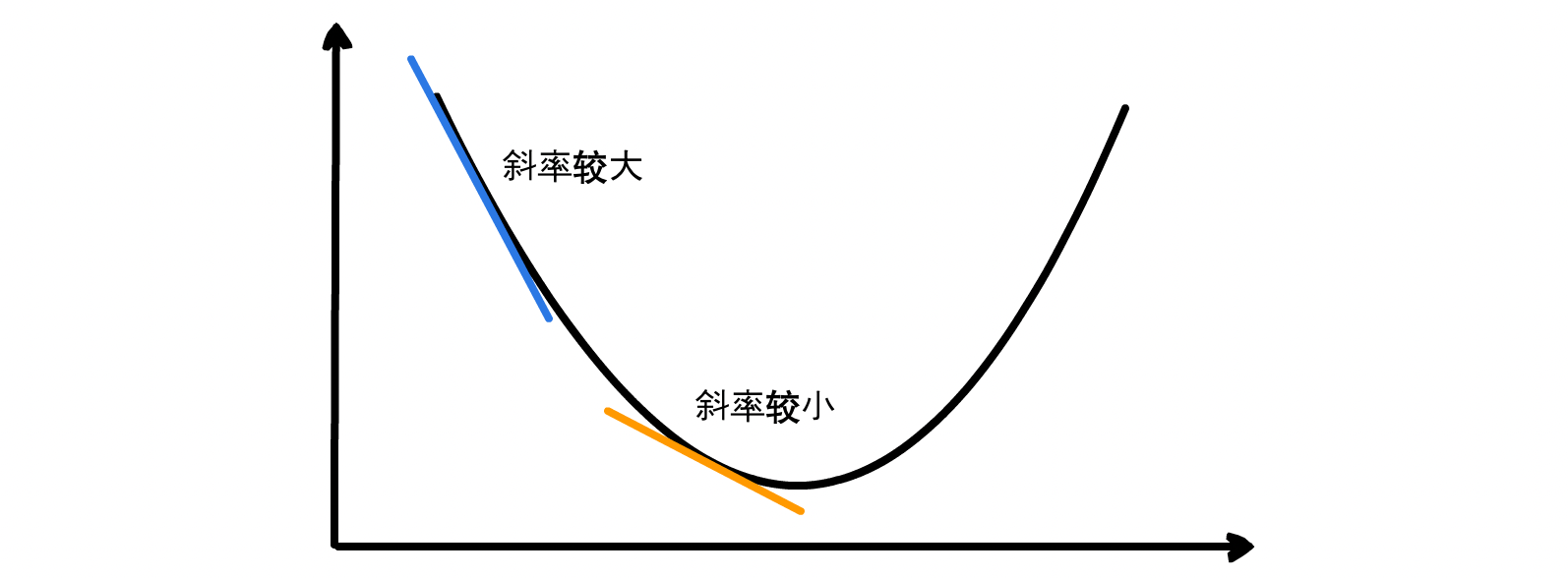
蛋先生：仔细观察上面的图，可以发现导数其实就是 x0 点处切线的斜率。而斜率反映了倾斜程度。所以导数的值越大，意味着在这一点上越陡峭，说明一点点 x 的变化会引起较大的 y 的变化，因此我们可以跨大一些的步子，更快地接近目标。相反，如果导数的值越小，步子也应该相应缩小一些，因为可能已经在目标附近了

走一步，往哪走？走多远？

丹尼尔：对于 x 的调整，我们既可以增大也可以减小，那如何判断应该增大还是减小呢？

蛋先生：我们的目的是让 y 的值尽量小，所以，如果导数为正，说明 x 变大时 y 也变大，我们就应该减小 x。如果导数为负，说明 x 变大时 y 变小，我们就应该增大 x

f’(x0) > 0 : x - ?
f’(x0) < 0 : x + ?

丹尼尔：那跨一步的距离应该是多少呢？

蛋先生：在机器学习中，如果梯度大，我们跨一步的距离就会相对大一些，这样可以更快地接近最小值；而如果梯度小，我们跨一步的距离就会相对小一些，因为可能已经在最小值附近徘徊了，跨步太大容易错过。对于一步实际的距离，我们可以使用 学习率 * 梯度 来控制，学习率 η 是一个超参数，需要我们自己来提供实际的值

f’(x0) > 0 : x - η * f’(x0) = x - η * |f’(x0)|
f’(x0) < 0 : x + η * f’(x0) = x - η * |f’(x0)|

丹尼尔：为什么要引入学习率呢？直接让一步的距离等于梯度的大小不行吗？

蛋先生：其实，确定每一步的合适距离是未知的，需要在实践中不断尝试和调整。因此，我们引入学习率这个参数，它就像一个“调节器”，允许我们通过调整其值来尝试不同的步长。这种调整可以手动进行，也可以通过一些自适应算法动态调节

丹尼尔：那么既然学习率是可以调整的，它会不会削弱梯度大小在决定步长时的作用呢？比如梯度大的乘个小的学习率，梯度小的乘个大的学习率

蛋先生：学习率虽然是可以调整的，但在同一轮迭代中，所有节点的学习率是相同的。因此，梯度的大小仍然能够反映出不同位置步长的相对差异

丹尼尔：我好像有点理解了，你们学会了吗？

蛋先生：你在跟谁说话？

丹尼尔：当然是阅读这篇文章的读者们啦！

蛋先生：好吧，那我们一起跟读者们 say goodbye 吧！

ヾ(￣▽￣)Bye_Bye

写在最后

亲们，都到这了，要不，点赞或收藏或关注支持下我呗 o(￣▽￣)ｄ