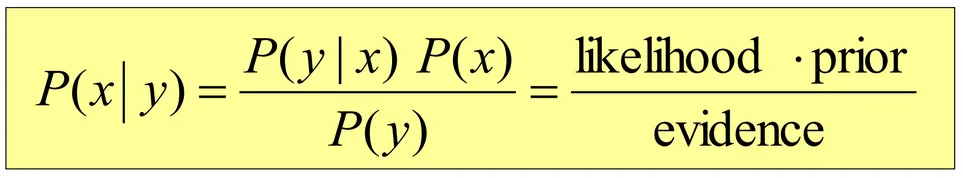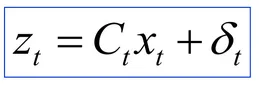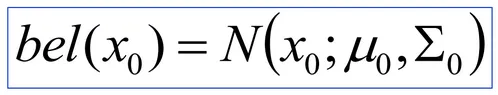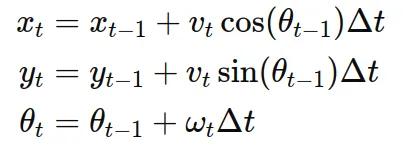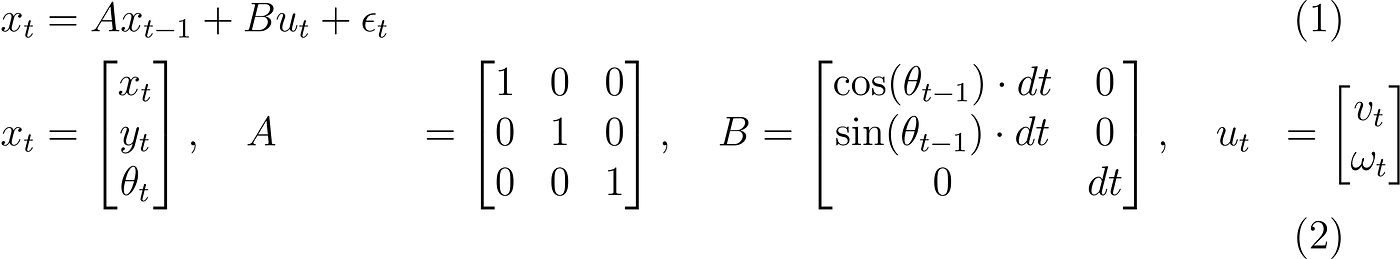基于卡尔曼滤波器的递归状态估计与ROS 2的应用讲解

这是我迄今为止最雄心勃勃的文章，旨在将超过40页的理论浓缩成一篇易于消化的文本（根据Medium的估计，可以在不到30分钟内读完）。这篇文章标志着一个系列的开端，该系列基于《概率机器人学》这本书展开。目标有两个：一是清晰地解释书中的概念，二是使用ROS 2和实际数据实现算法。如果您迫不及待，可以直接跳到实现部分的内容，但如果您对卡尔曼滤波器不太了解，建议从头开始完整阅读这篇文章。希望您喜欢阅读！

更新 2024年10月19日：高斯滤波器系列的最后一篇文章已发布。探索_ 信息滤波器_：一种强大且简化了状态估计计算的卡尔曼滤波器替代方案。

2024年08月09日更新：卡尔曼滤波三部曲的最后一篇文章已发布。了解无迹变换的强大之处及其在无迹卡尔曼滤波器中的应用。第一次接触卡尔曼滤波器？建议先从这篇文章开始。

更新日期 2024年5月30日：介绍_带有传感器融合的扩展卡尔曼滤波器_的后续文章已发布！第一次接触KF的读者？先读这篇文章。

机器人与环境的交互。出处：《概率机器人》（Probabilistic Robotics）

机器人通过感知和操控物理世界与其互动。这个环境或世界是一个动态系统，具有内部状况。通过传感器（比如摄像头、激光雷达等），机器人可以获得关于环境的信息（或观察结果）。由于这些传感器可能存在噪声，机器人无法完全了解环境，因此，它需要构建关于环境状态（以及自身状态）的内部信念。

机器人也可以通过其执行器（如夹爪、轮子等）改变其环境，从而导致环境状态的变化。就像传感器一样，执行器也带有噪声，因此机器人对状态的内部理解也需要相应地更新。这种交互（感知和影响世界）如图所示。

成功的机器人系统是那些能够感知并操控物理世界以完成有用任务的系统。为了完成这些任务，机器人需要能够应对环境中的巨大不确定性。因此，现代机器人学中最重要的基本问题之一就是状态估计问题。状态估计是指通过不确定的（有噪声的）和可能不完整的信息来估算机器人及其环境（如位置、方向、速度等）最可能的状态（如地标位置、其他对象位置和地图绘制）的过程。

计算信念的概率和解决状态估计最基本的方法是贝叶斯滤波器。因此得名，它利用贝叶斯滤波器来估计系统的状态。

你知道贝叶斯公式吗？它来自《概率机器人学课件》。

贝叶斯公式的标准化。摘自《概率机器人学讲义》

贝叶斯滤波器接收传感器观测值_z_和执行器控制动作_u_的输入流。它还需要一个传感器模型，根据观测值_z_推断状态x，以及一个动作模型，用于根据控制_u_预测状态x。最后，还需要机器人状态的先验分布。

贝叶斯滤波框架。来源：《概率机器人学》课件。

从上面的图中可以看到，传感器模型被描述为 p(z|x)，即给定当前状态 x，观测 z 的概率。例如，有一个机器人能够感知门的存在与否，如果观测到 z 是门，传感器模型会告诉我们，在机器人当前位置 x 下，存在门的概率有多大。

动作模型是 p(x|u, x’) ，表示在给定控制输入 u 和前一状态 x’ 的情况下，当前状态 x 的概率。例如，对于一个只能前进或后退的简单机器人，若给定控制输入 u = 1（即前进1米），则 p(x|u, x’) 描述了从上一位置 x’ 前进1米后到达当前位置 x 的概率。

p(x) 是我们当前的状态估计，而后验或信念是我们目标状态，在纳入观察 (z) 和控制输入 (u) 之后的估计，表示为 _p(x_t | u_1:t, z1:t)，其中 1:t 表示从初始时间 1 到当前时间 t 的所有观察和输入。

为了使贝叶斯滤波器变得可行，我们将状态的演变描述为马尔可夫链。这意味着过程的未来状态只依赖于当前状态，而不依赖于过去的事件。简单来说，给定当前状态，未来与过去无关。这是一个强大的简化条件，这使得建模和计算更加简单，因为它减少了依赖结构的复杂性。

马尔可夫假设。出自《概率机器人学》课件。

从贝叶斯公式出发，根据 _Bel(x_t) = p(x_t | u_1:t, z1:t) ，结合马尔可夫假设以及全概率公式，我们就可以得到贝叶斯滤波器的表达形式。

贝叶斯滤波器公式。出处：《概率机器人》的PPT。

如下所示，贝叶斯滤波公式可以通过此算法实施。在这个算法中，后验（即状态的新信念）的计算分为两步。第一步（第3行），我们通过考虑当前控制输入 _ut 从 t-1 时刻状态的变化来预测信念（因此 bel 上面有横线表示预测）。在第二步（第4行），我们使用传感器模型将时间 t 的观测值 _zt 纳入考虑，来更新我们的信念。注意，这个过程是在一个循环中完成的，其中预测基于前一时刻的后验 _bel(xt-1)，而更新则基于当前的预测 _bel^bar(xt)。因此，我们称其为递归状态估计过程。

贝叶斯过滤的一般算法。来源：《概率机器人》一书

目前还不清楚如何实现上述算法。不用担心这一点，因为贝叶斯滤波器更像是一种框架或模板，用于更高级滤波器的设计。只要你对它的工作原理有一些直觉，继续往下读，很快你就会看到卡尔曼滤波器是如何实现的，它是从贝叶斯滤波器发展而来的。

高斯滤镜家族

上一节介绍的贝叶斯滤波器虽然对于介绍状态估计这个主题很有帮助，但很少会像这样直接实现。不过，从它衍生的各种算法确实存在。每个算法家族在处理测量和状态转换概率以及初始信念的方式上有所不同，而这些差异又会影响后验概率（即更新后的信念）的表示方式。其中一类算法被称为高斯滤波器，卡尔曼滤波器就是其中之一。

高斯滤波器是贝叶斯滤波器最早和最受欢迎的实现之一。其基本概念是使用高斯分布来表示信念。在这种框架下，变量 x 代表状态，形成一个向量，向量中的值对应于被建模的各个方面。例如，在一个基本的状态表示中，若侧重于机器人姿态，x 可能包括机器人的位置（在世界坐标系中的 x 和 y 坐标，这里的 x 不是指状态变量 x）以及其方向 θ（theta）的值。

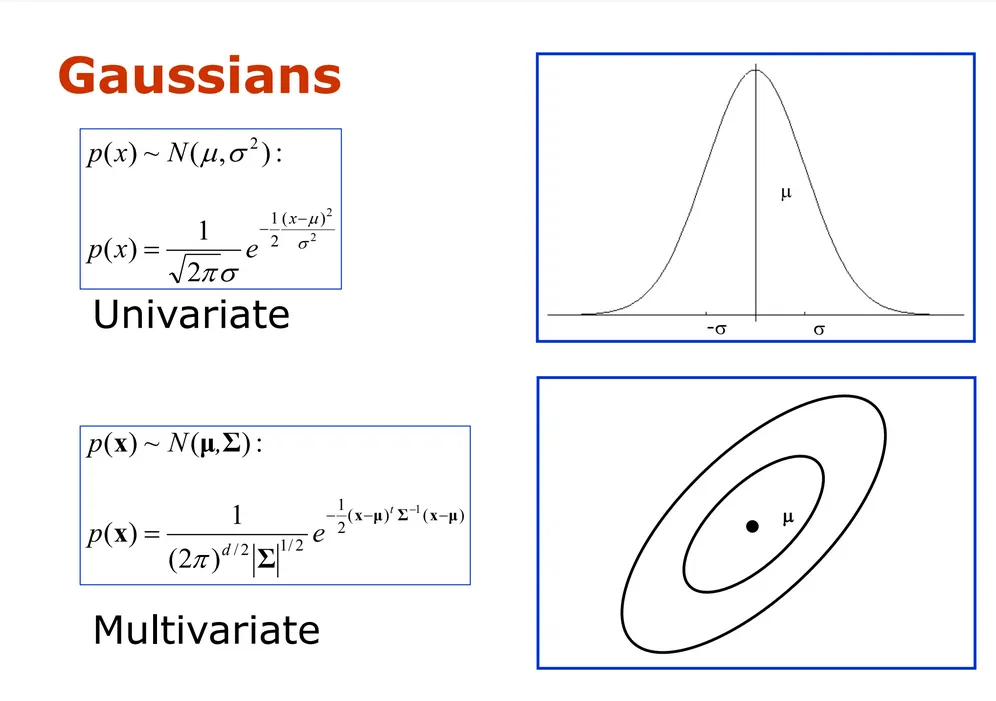
高斯函数。来源：《概率机器人学》幻灯片

为什么为 x 引入高斯表示呢？显而易见的问题是，如果我们对世界有完美的了解，那么 x 就足够了，然而实际上传感器和执行器都有噪声，我们只能通过自己的（或机器人的）信念来表示它。因此，我们不仅考虑 x ，而是讨论 p(x) ，即状态的概率。高斯分布，或者正态分布（因此用 N 表示），在这里发挥作用，使我们能够利用向量 μ （mu）和协方差矩阵 Σ （Sigma）来完全描述 x 的概率密度。

多元高斯。出自概率机器人课件

在这里， μ 被称为均值，代表平均值，即中心趋势，在我们实现的滤波器中，它将取状态 x 的值，确保 μ 和 x 有相同的维度。第二个参数 Σ ，即协方差，表示我们估计中的不确定性，即 Σ 的维度是 x 维度的平方。因此，机器人现在可以表达它对世界的看法，使用这两个参数，有效地描绘一个无法完全确定的环境。

让我们考虑一个非常简单的机器人，它只能沿一条直线移动。如下的单变量高斯分布就足够用来表示这种场景。其中 μ（用一条竖线来表示）是我们对机器人位置的信念（期望值），而由标准差（方差的平方根）决定的钟形曲线则反映了我们对位置的不确定性。结果是这样的概率密度函数，它将最高的概率分配给 μ，但并不是说 μ 的概率是100%。

一维高斯曲线。来源：Probabilistic Robotics 幻灯片

观察这个曲线，我们看到所有位于我们信念 μ 左侧和右侧的值也是可能的，尽管它们的概率逐渐减小。当我们离 μ 越远，可能性就越小。曲线还展示了方差的影响，如图所示。小的方差会造出一个更高更窄的曲线，将大部分概率集中到 μ 值周围，使该值更有可能。相反，大的方差会导致一个更矮更平的曲线，从而减少我们对信念的信心。结果是一种对一个真实状态难以捉摸的世界进行建模的方式。

不同的单变量正态分布。来源：维基百科正态分布页面

我们现在要深入探讨这篇文章的核心内容：卡尔曼滤波器。卡尔曼滤波器是一种广泛应用的贝叶斯滤波器实现，用于线性高斯系统。它只适用于连续状态，比如一个机器人的精确位置可以用它的 x 和 y 坐标来表示，这些坐标可以是任何实数。不过，它无法处理离散状态，比如机器人所在的楼层，用一个整数来标识。

使用高斯函数的一个原因是它们具有有利于滤波器实现的特性。当高斯随机变量经过线性变换时，结果依然是高斯随机变量。从一个由_μ_和_Σ_参数描述的变量_x_开始，可以通过将_x_乘以矩阵_A_并加上矩阵_B_来对其进行线性变换处理。结果变量_y_仍然是高斯分布，其均值为Aμ+B，协方差为AΣA^T。这确保了从高斯分布开始，仅通过线性变换后，结果依然保持高斯分布。

高斯分布变量的线性变换。来源：Probabilistic Robotics 课件

到了探索卡尔曼滤波器的时候了。记得之前提到的贝叶斯滤波器，它需要一个动作模型、一个传感器模型和一个先验条件。此外，回想一下马尔可夫假设，该假设表明未来状态仅取决于当前状态，而不依赖于整个历史。基于这一点，我们的动作模型，或者说状态转移概率，即 _p(x_t | u_t, xt-1)，定义了新的状态 _xt，基于先前的状态 _xt-1 和当前的控制输入 _ut。为了保持高斯特性，它必须是其参数的线性函数关系，并加入高斯噪声 _ϵt，以适应执行器固有的噪声。

通过行动模型估计状态x。出处：——Probabilistic Robotics讲义

传感器模型表示，或测量概率 (p(z_t | x_t))，它告诉我们给定某个时间点 (t) 的世界状态，在时间点 (t) 观测到 (z) 的可能性，也是用高斯分布来建模的，因此，它必须是对参数线性的，并添加高斯噪声以反映传感器噪声的特性。

通过传感器模型得到测量值 z 的可能性。来源：《概率机器人学》幻灯片。

最后，框架中最后缺失的部分是先验概率，即在时间点 t =0 时的初始状态。这个初始状态也必须遵循正态分布，也就是高斯分布。

初始的信念。出处：Probabilistic Robotics slides,

之前的三个假设确保了后验，即系统状态的更新信念，始终会是一个高斯分布，无论何时。这源于我们最初的信念，即一个高斯分布，经过时间的线性变换，结果仍为高斯分布。此外，传感器模型，同样是高斯分布的线性变换，更新信念。因此，我们始终在这个高斯分布的领域内。

所以不多赘述，如下的两图展示了卡尔曼滤波器算法及其各部分：

卡尔曼滤波器算法。来源：《概率机器人》。

卡尔曼滤波算法的组成部分。来源：《概率机器人》的幻灯片。

该滤波器旨在估计时间 t 的世界状态，并以时间 t-1 的先前状态为输入，该状态通过高斯参数 _μt-1 和 _Σt-1 描述。它还接收当前给定机器人的控制动作 (_ut)，这些指令将由执行器执行，以及通过机器人传感器获取的当前环境观察 _zt。

在第2行，滤波器预测机器人新状态，通过更新其两个参数。具体来说，它通过动作模型将过去的_μ_t−1_线性变换以预测_μ^bar_t_来更新预期值。此过程涉及使用矩阵_A_将状态向前推进，然后通过控制和矩阵_B_的乘积来进一步更新状态，以纳入控制的影响。噪声_ϵ_t_是高斯分布的，均值为0，协方差为R，所以，我们向状态的预期值中添加了0。

在第3行中，状态的第二个参数被更新以完成预测。按照高斯线性变换的规则，将__Σ_t-1_向前投影，得到__Σ^bart\。然后添加噪声\ϵt__的协方差矩阵\_Rt\。这标志着卡尔曼滤波器预测步骤的完成。

从第4行到第6行，卡尔曼滤波器的更新步骤被执行，将测量值整合进来以改进我们对于状态的估计。在第4行中，变量_Kt，即卡尔曼增益，被计算出来以确定测量值影响新状态估计的程度。本质上，预测状态的协方差_Σ^bar_t_通过乘以_C_t_的转置，将其从状态空间转换到了测量空间，然后除以其不确定性之和。这些不确定性包括状态不确定性（投影到测量空间中）和测量不确定性（由测量噪声协方差_Q_t_表示）。

在第5行中，我们通过调整均值估计 _μ^bart 来融合测量值 _zt 到 _μ^bart 中，从而更新后验 _μt。这种调整基于创新，即传感器测量值 (_zt) 与根据传感器模型 (_C_t .μ^bart) 的预测之间的差距。卡尔曼增益 (_Kt) 决定了要融合多少创新。简单来说，如果我们对传感器的准确性信心不足（由较大的测量协方差 _Qt 表示），_Kt 将较小，从而导致较少地吸收创新量。相反，如果我们对传感器的准确性信心较高，则更多的测量值将被用于更新均值。

在第6行中，滤波器调整后验协方差_Σt，以反映从测量中获取的信息。这一调整按卡尔曼增益的比例进行，并取决于我们对传感器的信任程度。增益越大意味着对传感器越信任，协方差减少得越多，确定性也就越高。相反，如果传感器噪声较大且信任度较低，协方差减少得少，保留更多的不确定性。然而，无论传感器是否可靠，协方差总是减少的，这反映了传感器提供的有用信息。

算法在第7行通过返回后验来结束。当在循环中迭代调用时，时间 t-1 的后验成为时间 t 的输入，我们可以递归估计机器人的状态及其环境。所有步骤和公式的完整推导超出了本文的讨论范围，但我鼓励读者参考建议的材料。介绍了卡尔曼滤波器的基础后，现在我们可以探讨其实际应用了。

为了演示卡尔曼滤波器，我开发了一个ROS 2包，该包使用我的SHL-1机器人记录的真实世界的记录数据（以ROS 2 bag的形式）。在这个实现中，我们要估计的目标状态是机器人的姿态（位置和方向）（x, y, θ），所使用的传感器是轮子里程计，它通过轮子运动计算出机器人的位置和方向（x_odom, y_odom, θ_odom）。首先，你有两个选择：自己运行代码或仅仅观看视频演示。如果你选择运行代码，我将提供基本的设置指南。如果你只想观看视频，可以直接跳过这一部分。

首先，你需要 ROS 2。你可以在这里找到相关说明，关于如何在 Ubuntu Jammy Jellyfish (22.04) 上安装 ROS 2 Humble here。对于其他版本的 Ubuntu 或在其他操作系统上，请参阅官方提供的 ROS 2 文档。

要拿到数据，你需要从这个链接下载ROS 2 bag。确保在使用前解压文件。

最后，你需要克隆然后构建ROS 2包。你可以按照下面的步骤操作。记得将ros2_ws替换为你自己的ROS 2工作区。

    # 安装一些依赖项  
    sudo apt install python3-pykdl  

    # 切换到 ros2 工作空间的 src 目录  
    cd ros2_ws/src  
    # 克隆包  
    git clone https://github.com/carlos-argueta/rse_gaussian_filters.git  
    cd ..  
    # 仅构建 rse_gaussian_filters 包  
    colcon build --symlink-install --packages-select rse_gaussian_filters

让我们来看看代码中最重要的部分。我们将略过ROS 2的细节。如果你是ROS的新手，我推荐你跟着这里提供的初级教程学学，这些教程足够让你理解整个代码。

卡尔曼滤波器的第一个关键步骤是初始化。这个经常被忽视的步骤可能会决定状态估计的成败。

    # 初始化卡尔曼滤波器如下  
    mu0 = np.zeros(3)  
    Sigma0 = np.eye(3)  
    proc_noise_std = [0.02, 0.02, 0.01]  
    obs_noise_std = [0.02, 0.02, 0.01]  
    self.kf = KalmanFilter(mu0, Sigma0, proc_noise_std, obs_noise_std)

我们的简单卡尔曼滤波器对象使用先验概率分布N(μ0, Σ0)进行初始化，这代表了我们对机器人状态的初始信念。由于我们要估计机器人的姿态，mu0被初始化为向量值(0.0, 0.0, 0.0)。这表明我们并不真正知道机器人的全局位置，假设它是这样的位置：位于原点并且面向正x轴（ROS默认设置）。如果有地图和GPS传感器，我们可以用首次获得的GPS坐标来初始化先验。初始协方差矩阵被设定为单位矩阵，这实际上表示了我们对先验的一些不确定性。如果有GPS，我们还可以用该传感器报告的协方差作为初始不确定性。

另一个关键的初始化参数是过程噪声协方差 R 和观测噪声协方差 Q，分别由相应的向量 _proc_noisestd = [0.02, 0.02, 0.01] 和 _obs_noisestd = [0.02, 0.02, 0.01]（请参见下面的代码以获取更多细节）。这些向量包含了动作噪声对 x，y 和 theta 影响的标准差，既适用于动作模型也适用于传感器模型。对于动作模型来说，它们表示由于车轮执行器的不精确性导致预测位置的不准确性；而对于传感器模型来说，它们则表示轮子里程计传感器的噪声导致的观测里程计的不精确性。

一个更复杂的卡尔曼滤波器实现通常会包含更多的参数，但这里所列举的内容已经足以初学者理解这个主题。类似于最初的信念，我们分配给噪声协方差的值大多是任意设定的。理想情况下，我们可以咨询我们所用传感器和执行器的制造商以获取关于设备精度的准确数据，从而根据这些数据来定义更准确的初始值。下面展示的 KalmanFilter 对象的构造函数利用所提供的参数初始化机器人的信念和噪声协方差。它还获取到动作模型矩阵 A 和 B ，以及传感器模型矩阵 C 。

    def __init__(self, initial_state, initial_covariance, proc_noise_std=[0.02, 0.02, 0.01], obs_noise_std=[0.02, 0.02, 0.01]):  

      self.mu = initial_state  # 初始状态
      self.Sigma = initial_covariance  # 初始不确定性

      self.A, self.B = velocity_motion_model()  # 运动模型，返回 A 和 B 矩阵

      # x, y, theta 的噪声标准差（过程或动作模型的噪声）
      self.proc_noise_std = np.array(proc_noise_std)  
      # 过程噪声协方差 R
      self.R = np.diag(self.proc_noise_std ** 2)  # 过程噪声协方差

      # 观测模型 C
      self.C = odometry_observation_model()  # 定义使用的观测模型

      # x, y, theta 的噪声标准差（观测或传感器模型的噪声）
      self.obs_noise_std = np.array(obs_noise_std)  
      # 观测噪声协方差 Q
      self.Q = np.diag(self.obs_noise_std ** 2)

通过实现卡尔曼滤波的一个方面，我们可以更清晰地理解如何构建模型矩阵。虽然我们已经认识到矩阵 A 、B 和 C 的必要性，但我们还没有讨论如何编码它们。在动作模型（也称为过程）的背景下，矩阵 A 描述了从时间 t-1 到 t 的状态转换，不考虑噪声和控制影响，而矩阵 B 则展示了控制动作如何影响状态变化。定义这些矩阵取决于被估计的状态的特性。在我们的场景中，我们估计机器人的姿态，这些矩阵描述了机器人随时间姿态变化的运动特性。

速度模型方程

使用矩阵和向量的速度运动模型

存在多种表示机器人运动的模型，其中最常用的一种是速度运动模型（见上图和下方代码）。在此模型中，矩阵A对状态没有影响，所以它就是单位矩阵，不会改变任何状态。矩阵B则描述了如何通过施加控制输入，比如平移速度(v)和旋转速度(ω)，来改变状态。换句话说，新的状态由之前的姿态加上通过控制输入导致的平移和旋转，再加上一些噪声。

def 线性速度运动模型():  # 定义线性速度运动模型
    def 状态转移矩阵_A():  # 定义状态转移矩阵A
        A = np.eye(3)

        return A

    def 控制输入矩阵_B(mu, delta_t):  # 定义控制输入矩阵B
        theta = mu[2]
        print("角度和时间间隔为：", theta, delta_t)
        B = np.array([
            [np.cos(theta) * delta_t, 0],
            [np.sin(theta) * delta_t, 0],
            [0, delta_t]
        ])

        return B

    return 状态转移矩阵_A(), 控制输入矩阵_B

最后，我们定义传感器模型矩阵 C。该矩阵的主要作用是将我们的状态从状态空间转换到观测空间，从而让我们能够将新的信息整合到状态估计中。所使用的轮式里程计通过车载轮速传感器计算出机器人的位置和方向，因此可以直接将状态空间映射到观测空间，无需额外转换，矩阵 C 就是单位矩阵。然而，如果我们仅限于使用原始的轮编码器数据，这种原始数据通常测量轮子的旋转次数，那么就需要一个转换过程，将矩阵 C 变为不同的形式。

    import numpy as np  

    def 里程计观测模型():  
     return np.eye(3)

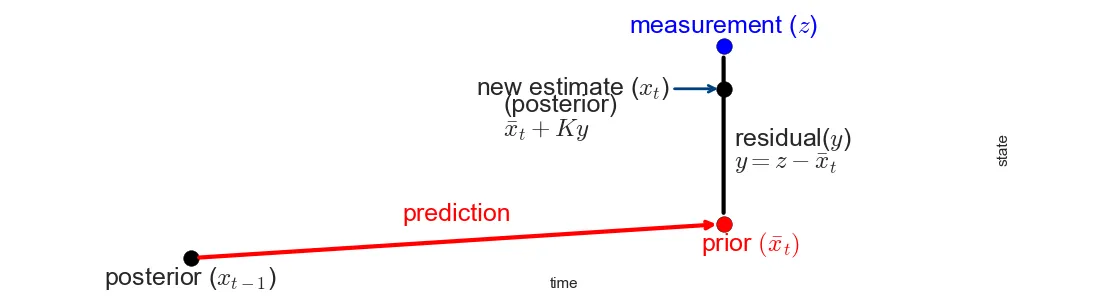
以下是卡尔曼滤波器对象的剩余代码。在预测步骤中，我们使用速度模型更新均值，同时加入控制的影响，同时协方差被更新，以反映执行器噪声引起的不确定性。接着，在更新步骤中，按照卡尔曼增益的比例，将预测状态与观测之间的差异（称为创新或残差）按比例加到均值中。这一调整的程度取决于我们对传感器的信心，即协方差矩阵_Q_的定义。

一张图解释了卡尔曼滤波器。来源：《Kalman和贝叶斯滤波器》（Python版）——Kalman和Bayesian Filters in Python

    def predict(self, u, dt):  
      # 预测状态  
      self.mu = self.A().dot(self.mu) + self.B(self.mu, dt).dot(u)  
      # 预测协方差  
      self.Sigma = self.A().dot(self.Sigma).dot(self.A().T) + self.R  

      return self.mu, self.Sigma  

    def update(self, z):  
      # 计算卡尔曼增益因子  
      K = self.Sigma.dot(self.C.T).dot(np.linalg.inv(self.C.dot(self.Sigma).dot(self.C.T) + self.Q))  
      # 更新状态  
      self.mu = self.mu + K.dot(z - self.C.dot(self.mu))  
      # 更新协方差  
      self.Sigma = (np.eye(len(K)) - K.dot(self.C)).dot(self.Sigma)  

      return self.mu, self.Sigma  

要运行卡尔曼滤波器，你需要打开三个不同的终端。

在终端 1 中（将 _ros2ws 替换为您实际的工作空间），执行以下命令以打开 Rviz 并查看机器人看到的画面。

source ~/ros2_ws/install/setup.bash  
运行上述命令后，将会加载ROS2的工作环境设置。接着，通过执行 `ros2 launch rse_gaussian_filters rviz_launch.launch.py` 命令来启动rviz界面。

在第二个终端中运行以下命令来运行卡尔曼滤波。开始时不会有任何输出，直到你播放ROS 2 回放文件。

source 源环境脚本以设置ROS2工作空间的环境变量, 然后运行名为kf_estimation的ros2节点从rse_gaussian_filters包中。

在终端3中转到你提取的ROS 2 bag文件的目录，并用以下命令播放它。可以忽略一些警告，例如“忽略话题‘/navrelposned’，因为找不到相应的包‘ublox_msgs’”。

运行ROS2回放包命令:

ros2 bag 回放 linkou-2023-12-27-2-med --clock  # 使用系统时钟

在第一个视频中，展示了使用默认噪声参数 _proc_noisestd = [0.02, 0.02, 0.01] 和 _obs_noisestd = [0.02, 0.02, 0.01] 的卡尔曼滤波器。在这种情况下，运动和传感器模型都被认为同样可靠，不确定性相对较低。

使用默认参数的卡尔曼滤波器

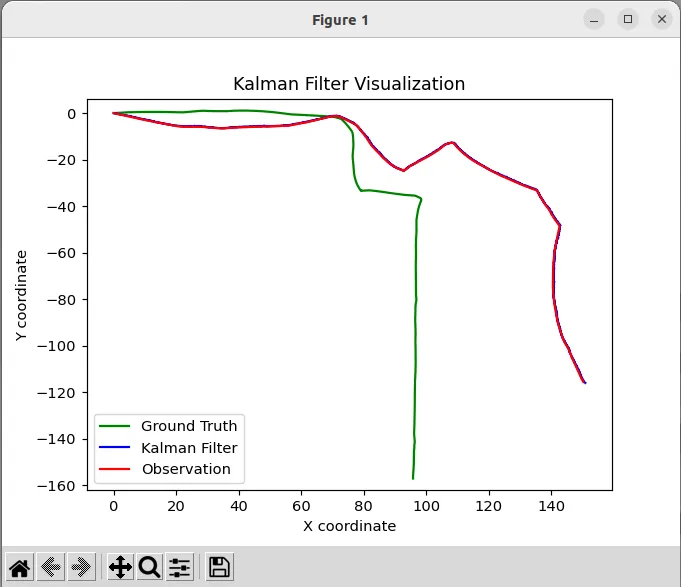
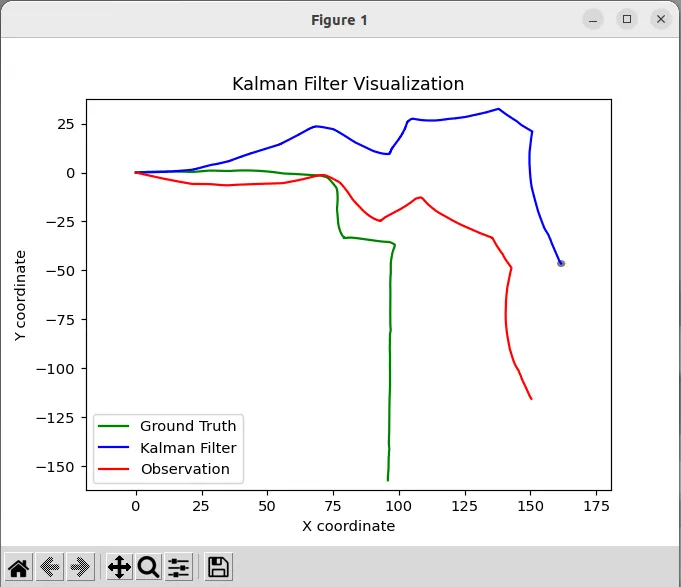
分析最终的情节表明，预测的姿态（蓝色） ，似乎与基于车轮里程计计算出的姿态非常接近，尽管这种感知在某种程度上受到图的比例尺的影响。

具有默认参数的卡尔曼滤波器输出结果

更加详细的检查表明，在滤波最初的10秒内，预测的姿态与观测结果并不完全吻合。动画中观察到的阶梯状模式是滤波器的预测-更新循环过程的结果。在预测阶段，蓝色线会偏离观测结果，因为它遵循了运动模型。然而，在更新阶段，由于对观测结果给予了同等的信任，蓝色线会被拉回到更接近观测数据的位置。

使用默认参数时，卡尔曼滤波器运行最初的10秒。

与地面实况（绿色）相比，滤波器的表现不尽理想。卡尔曼滤波器与其他滤波器一样，并非万能。这反映了机器学习中的一个常见说法：“输入数据质量差，输出结果也会差。”在这种情况下使用的轮式里程计存在较大的漂移误差，通常被认为不适合长时间内准确地跟踪机器人姿态。相比之下，地面实况则是通过将轮式里程计和IMU（惯性测量单元）数据融合得出的，从而校正了里程计的误差。在未来的文章中，我计划展示如何通过在更新步骤中引入IMU数据来增强卡尔曼滤波器，以提供更精确的估计。

在下一个视频中，我们将噪声参数设置为 _proc_noisestd = [0.002, 0.002, 0.001] 和 _obs_noisestd = [1000.02, 1000.02, 1000.01]。通过这种设置，我们非常相信我们的动作预测模型，但认为我们的轮式里程计存在很大的噪声。接下来的视频中显示的结果应该不会让大家感到惊讶。机器人预测的轨迹（蓝色）很快偏离了观察结果（红色），因为基于运动模型的预测占了主导地位，而更新步骤中几乎没用到观察结果。

带有高观测噪声的卡尔曼滤波器

卡尔曼滤波在高观测噪声下的输出

在过程的前10秒内，我们注意到滤波器已经开始很大程度上忽略观测。似乎仅靠运动模型就能更好地描述机器人的实际运动，但从最终输出（如上图所示）可以看出，它很快就偏离了真实轨迹。最后，请注意围绕最终预测姿态的椭圆，这表示我们的状态协方差Σ。与之前的场景相比，这里的椭圆几乎不可见，而在此情况下，椭圆明显较大。这种尺寸的增加归因于观测值的高噪声水平，反映了状态估计的更高不确定性。

运行卡尔曼滤波器最初的10秒，观测噪声很大

在最终调整中，我们将噪声参数调整为 _proc_noisestd = [1000.02, 1000.02, 1000.01] 和 _obs_noisestd = [0.002, 0.002, 0.001]。此设置告诉滤波器我们对运动模型的信心不高，但完全信任轮式里程计的读数。

具有高运动模型噪声的卡尔曼滤波器

具有高动态模型噪声的卡尔曼滤波器输出

最终结果与使用默认值时得到的结果非常相似，这并不令人惊讶。在两种情况下，与轮式里程计测量相关的噪声都很低，导致滤波器紧密跟踪测量值。此外，实验前10秒显示出类似默认情况下的阶梯状模式，但因为我们的运动模型可信度较低，这种模式没有那么明显。

在高运动模型噪声情况下，卡尔曼滤波器运行最初的10秒钟。

在这篇文章中，作为高斯滤波器系列的第一篇，我介绍了卡尔曼滤波家族中最基本的成员——线性卡尔曼滤波器。虽然这个实现使用了实际机器人数据，并在像ROS 2这样的生产级系统中运行，线性卡尔曼滤波器主要被用作教育工具，通常不推荐用于实际应用中。其主要限制在于假设过程和测量模型都是线性的。这种线性的假设体现在两个模型的方程式里，以下再次列出供参考。

状态 $x_t$ （或 $xt$ 状态）是 $X{t-1}$ 和 $u_t$ 的线性函数。出处：《概率机器人学》PPT。

预测测量值 $z_t$ 是 $x_t$ 的一个线性函数，这出自《概率机器人学》幻灯片。

如卡尔曼滤波器介绍中所强调的，保持方程线性的主要原因是保留状态概率分布的高斯特性。非线性运算会使这些分布变为非高斯分布，进而破坏滤波器的递归框架和简单更新方程。问题在于，许多现实中的系统是非线性的。例如，本实现的速度模型（如下重述）由于含有与机器人姿态和位置变化相关的三角函数，因此该模型是非线性的。

x和y坐标的变化与θ方向的三角函数有关。

由于状态转移矩阵是为线性动态系统设计的，它无法准确跟踪非线性系统的演变。这种不准确性会随着时间推移导致误差累积和估计偏差越来越大，特别是在长时间内。此外，滤波器在描述非线性系统固有不确定性方面存在局限性，这可能导致实际不确定性被低估。此外，卡尔曼增益可能无法被准确计算。因此，滤波器可能会过分依赖噪声测量，或对实际状态变化反应迟缓。

在状态转换或测量本质上是非线性的情况下，会使用线性卡尔曼滤波器的替代方案，例如扩展卡尔曼滤波器（EKF）或无迹卡尔曼滤波器（UKF）。这些滤波器通过近似或转换来处理非线性，并尽可能保留概率分布的高斯特性。在本系列的下一篇文章中，我将介绍扩展卡尔曼滤波器（EKF），探讨其功能及其如何应对非线性系统带来的挑战。

这里有一些我参考过的关于卡尔曼滤波的优秀材料：

1. 卡尔曼滤波、H∞滤波及非线性滤波的状态估计
2. 机器人状态估计方法
3. 用Python实现的卡尔曼和贝叶斯滤波器

4. 基于概率的机器人学

   希望这篇文章对你来说是有帮助的。有任何反馈，请随时留言。我计划推出一系列更深入的课程，不仅涵盖这个主题，还将包括未来的话题，包括视频教程、编程项目等。这些课程可能是付费的。如果你感兴趣，请在评论区留言，让我知道一下。

更新公告 2024年9月8日：卡尔曼滤波三部曲的最后一篇文章已发布。了解UKF变换的惊人力量及其在Unscented Kalman Filter中的应用：UKF变换的强大之处。如果您是卡尔曼滤波器的新手，建议先阅读当前的文章。

2024年05月30日更新：介绍带传感器融合技术的扩展卡尔曼滤波器的后续文章发布了！对卡尔曼滤波器不熟悉的读者，请先阅读这篇文章。

想联系我吗？在我的LinkedIn上联系我：https://www.linkedin.com/in/carlos-argueta/