用Python探索可解与不可解方程的问题

一位正在主持意大利文艺复兴时期数学竞赛的编程语言Python——来源：https://openai.com/dall-e-2/。其余图片均由作者提供。

为什么我们可以轻松地解一些方程，却另一些似乎无解？另外，为什么这种知识对我们保密？

作为数据科学家、应用科学家和工程师，我们这些经常构建数学模型的人，给定一个 x 的值，我们可以计算出 y。例如，如果 x = 3，那么 y = 9，就像这样。

我们也可以反过来使用这个模型。从 y = x² 开始，我们重新排列以解出 x ：x = ±√y。如果 y = 9，那么 x = ±3。表达式 x = ±√y 是一种 封闭形式的解 —— 使用有限常规运算和函数组合的表达。

然而，并非所有的模型都是如此简单。有时，我们会遇到无法直接解出_x_的封闭形式表达式的方程。在这种情况下，我们可能会听到“这无法直接求解，你需要使用数值方法”。数值方法非常强大，可以提供精确的近似。但是，这让我（或许也让你）感到沮丧的是，似乎没有人愿意说明什么时候可以得到封闭形式的解，什么时候不行。

伟大的约翰内斯·开普勒也和我们一样感到沮丧。他提出了行星运动模型。

• 设 y 等于 x 减去 c 乘以 sin(x) 的结果

这个方程将物体在轨道上的位置（x）转换为对应的时间（y）。开普勒试图找到一个封闭形式的解，以通过 x 将时间转换为位置。然而，即使过了400年，我们最好的办法仍然是使用数值方法。

在这篇文章中，我们将理解何时可以期望得到封闭形式解。唯一能够严格确定这一点的方法是通过使用比如伽罗瓦理论、超越数论和代数几何。这些主题远远超出了我们通常所学的范围，作为应用科学家和工程师。

相反，我们不会深入探讨这些高级领域，而是会投机取巧。我们将使用SymPy，一个基于Python的计算机代数系统，探索不同类型的方程式，看看它能否直接求解这些方程。同时，我们也会应用数值计算方法。

我们将探讨结合多项式、指数函数、对数函数和三角函数的方程。在这个过程中，我们将发现一些常常难以找到封闭形式解的特定组合。你会看到，如果你想创建一个有（或没有）封闭形式解的方程，你应该避免（或试试）以下的方法：

• 五次或五次以上的多项式
• 混合使用 x 与 exp(x) 或 log(x) — 如果兰伯特 W 函数不被允许使用
• 在同一个方程中结合使用 exp(x) 和 log(x)
• 某些频率可公度的三角函数对
• 许多具有不公度频率的三角函数对
• 混合使用三角函数与 x 、 exp(x) 或 log(x)

旁注 1：我不是数学家，我的 SymPy 脚本也不算很高深。如果你发现了任何错误或遗漏的资源，请原谅我的疏忽。请与我分享，我会很高兴添加注释。

旁注 2：Welch Lab 最近的视频《开普勒的不可能方程》（Kepler’s Impossible Equation）让我想起了我对何时能找到闭式解的困惑。这个视频激发了以下的探讨，并为我们提供了第一个实例。

想象你现在是约翰内斯·开普勒的程序员。他设计了如下轨道运动模型。

y = x − c sin(x)

其中：

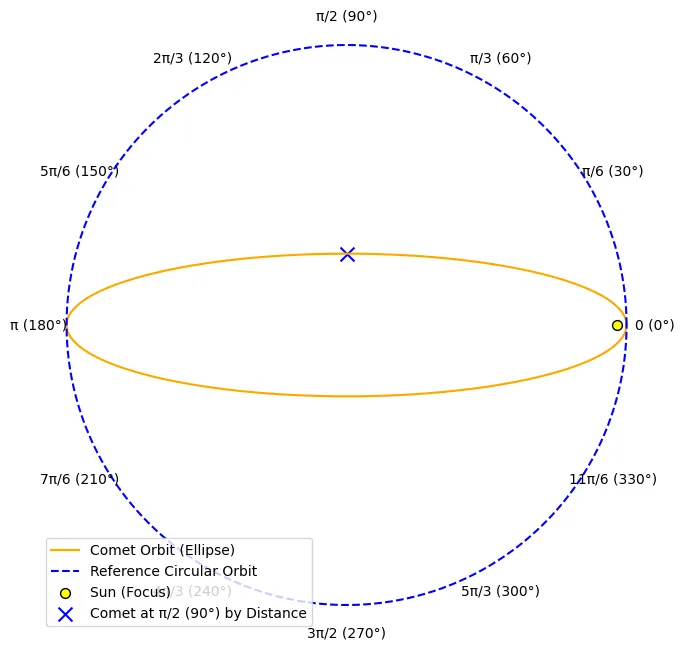
• x 是物体在其轨道上的位置。我们用角度（弧度）来表示这一位置。角度从物体最接近太阳时开始为 0 弧度。当物体经过四分之一的轨道距离时，角度为 π/2 弧度 (90°)。当它走过轨道一半的距离时，角度为 π 弧度 (180°)，以此类推。请记住，弧度的范围是从 0 到 2π，而不是 0 到 360°。

• c 是轨道的偏心率，范围从 0（完美的圆形）到接近 1（高度拉长的椭圆）。假设开普勒观察到一颗彗星，它的 c 值为 0.967。

• y 是物体在其轨道上的时间。我们用角度（弧度）来表示这一时间。例如，如果彗星的轨道周期为 76 地球年，那么 π/2 (90°) 对应于 76 年的四分之一，也就是 19 年。π (180°) 对应于 76 年的一半，也就是 38 年。2π (360°) 对应于整个 76 年的轨道周期。

此图显示了彗星在π/2弧度（90°），即在其轨道四分之一处的位置。

开普勒想知道当彗星到达 π/2 弧度（90°）的位置时的时间。你编写并运行了这段 Python 代码如下所示：

    import numpy as np  

    def kepler_equation(x):  
        return x - c * np.sin(x)  

    c = 0.967  
    位置弧度 = np.pi / 2 # Position in radians, equivalent to 90 degrees  
    时间弧度 = kepler_equation(位置弧度)  
    轨道周期地球年 = 76 # Orbital period in Earth years  

    t_地球年 = (时间弧度 / (2 * np.pi)) * 轨道周期地球年  
    print(f"彗星从 0 到 π/2 弧度的运动大约需要 {t_地球年:.2f} 年。")

你向（汇报对象）汇报一下：

彗星从0到π/2弧度的移动差不多需要7.30个地球年的时间。

备注：它只用不到公转周期的10%的时间就走完了25%的轨道距离，因为它靠近太阳时会加速。

行善未必有好报。开普勒对结果感到好奇，给你安排了一个新任务：“过了20个地球年后，你能算出彗星在轨道上的位置吗？我想知道它在轨道上的位置，以弧度表示。”

“行吧，”你这么一想，“我用点高中学的代数就可以了。”

首先，你将大约20地年转换为弧度。

• 时间弧度值 = (20除以76)乘以2π = (10除以19)π

接下来，你调整开普勒方程，令其等于0。

• x − 0.967 sin(x) − (10/19)π = 0

现在你想找使这个方程为真的_x_的值。你决定画出它的图像来看看它在哪里穿过零。

    import numpy as np  
    import matplotlib.pyplot as plt  

    c = 0.967  
    time_earth_years = 20  
    orbital_period_earth_years = 76  
    time_radians = (time_earth_years / orbital_period_earth_years) * 2 * np.pi  

    def function_to_plot(x):  
        return x - c * np.sin(x) - time_radians  

    x_vals = np.linspace(0, 2 * np.pi, 1000)  
    function_values = function_to_plot(x_vals)  
    plt.figure(figsize=(10, 6))  
    plt.axhline(0, color='black', linestyle='--') # y=0 的虚线  
    plt.xlabel("弧度位置")  
    plt.ylabel("数值")  
    plt.title("求解 x - c sin(x) - y 的图像")  
    plt.grid(True)  

    plt.plot(x_vals, function_values)  
    plt.show()

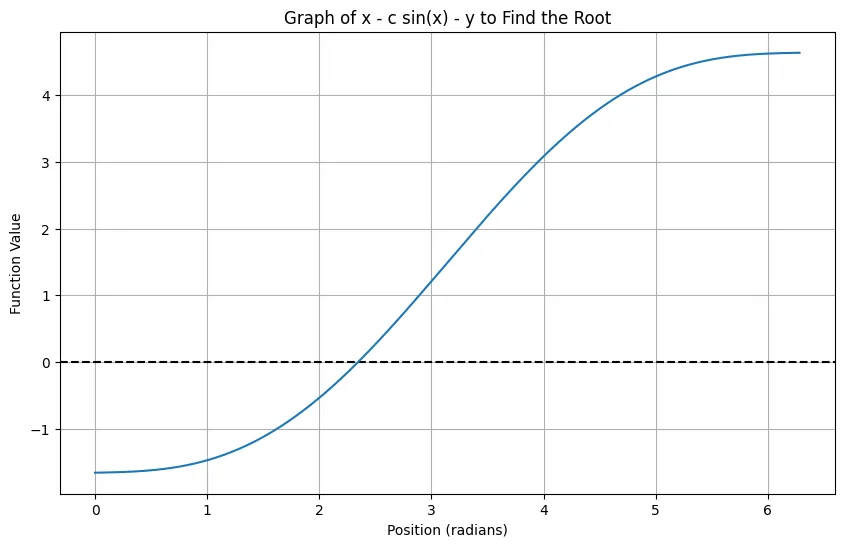
到目前为止一切顺利。图表显示_x_确实存在解。但是当你尝试通过代数重新排列方程来解_x_时，你却遇到了难题。当方程中既有_x_又有sin(x)时，你怎么单独解出_x_呢？

“这也没问题，”你想着，“我们有Python，Python自带的SymPy包，是一款强大且免费的计算机代数系统。”

你把这个问题交给 SymPy 处理：

    # 提示：此代码将失败。
    import sympy as sym
    from sympy import pi, sin
    from sympy.abc import x

    c = 0.967
    time_earth_years = 20
    orbital_period_earth_years = 76

    time_radians = (time_earth_years / orbital_period_earth_years) * 2 * pi
    equation = x - c * sin(x) - time_radians

    solution = sym.solve(equation, x)
    #^^^^^^^^^^^^^这里会报错^^^^^^^^^^^^^^
    print(solution)

遗憾的是，它却报错了。

未实现错误: 多个生成器 [x, sin(x)]。目前还没有实现用于求解方程 x - 967*sin(x)/1000 - 10*pi/19 的算法。

SymPy 在求解方程方面表现得很好，但并不是所有的方程都能用所谓的 解析解 来表达。即解可以用有限数量的初等函数（加法、乘法、根、指数、对数和三角函数）来表示。当我们将一个像 x 这样的项与一个像 sin⁡(x) 这样的三角函数项结合时，要将 x 解出可能会变得根本不可能。换句话说，这种混合类型的方程通常没有解析解。

这没有问题。从图中我们知道存在一个解。SymPy可以使用数值方法帮我们无限接近这个解。例如，我们使用SymPy的nsolve()函数：

    import sympy as sym  
    from sympy import pi, sin  
    from sympy.abc import x  

    c = 0.967  
    time_earth_years = 20  
    orbital_period_earth_years = 76  
    time_radians = (time_earth_years / orbital_period_earth_years) * 2 * pi  
    equation = x - c * sin(x) - time_radians  

    initial_guess = 1.0   # 数值求解器的初始猜测值  
    position_radians = sym.nsolve(equation, x, initial_guess)  
    print(f"{time_earth_years} 地球年之后，彗星在其轨道上将行进 {position_radians:.4f} 弧度 ({position_radians * 180 / pi:.2f}°)。")

哪些报道呢？

20个地球年之后，彗星将沿着它的轨道移动2.3449弧度，134.35°。

我们可以用一个表格来总结一下结果，如下：

我们确定没有闭式解吗？我们在否定的答案后加了个问号。这提醒我们，SymPy失败了，并不意味着没有闭式解的数学证明。我们将最后一列命名为“A 数值”来提醒自己它代表一个数值解，可能还有其他的解。

在这部分，我们探讨了开普勒方程并发现了用封闭形式求解它的难题。Python的SymPy库证实了我们难以用封闭形式求解，最终我们只能依赖数值解法。

这给了我们一个没有明显封闭形式解的方程的例子。但这常见吗？是否存在某些方程类，我们总是能够找到封闭形式的解，或者永远无法找到？让我们通过研究另一种方程类型——多项式，进一步探索。

例如方程 x ² − x − 1 = 0，这种多项式方程是数学建模中的可靠锤子——虽然简单却十分强大。我们在学校里都学过如何解这类含有 x ² 的二次方程。

500年前，在意大利文艺复兴时期，解高次多项式问题成为了公众娱乐的焦点。像塔尔塔利亚和卡尔达诺这样的数学家在公开的数学决斗中竞争荣誉和认可。这些竞赛为三次（立方）和四次（四次方）多项式找到了解法。那么五次多项式呢？

咱们用SymPy来研究一下一些多项式例子：

对于次数不超过四次的多项式，我们总能找到这样的解，这些解可以用基本算术运算和根（如平方根或立方根）的有限的表达形式表示。

多项式的解的数量绝不会超过它的次数。然而，某些解可能包含 i ，即 -1 的平方根，这指的是复数。等一下再详细说说。

关于五次及更高次的多项式呢？我们总能找到封闭形式的解吗？答案是混合的。有时候，我们可以找到。当存在这样的解时，例如上面的 x ⁵+1=0，SymPy 通常会找到它。

然而，在其他情况下，例如对于方程 x ⁵-x -1=0，SymPy 无法找到一个封闭形式的初等解。Évariste Galois 著名地证明了对于一般的高次多项式，不存在封闭形式的解。然而，SymPy 在特定方程上的失败并不能证明没有封闭形式的解。因此，对于这个例子，我们在答案后添加一个问号，回答“没有？”。

为了进一步探索，当我们输入 x ⁵-x -1=0 时，让我们看看 SymPy 具体做了什么：

    import sympy as sym  
    from sympy.abc import x  

    equation = x**5 - x - 1  
    solution = sym.solve(equation, x)  
    print(solution)

添加sympy库，并定义x为符号变量。然后定义方程和求解方程的解并打印解。

结果是：

这表示方程$x^5 - x - 1 = 0$的五个解：[CRootOf(x**5 - x - 1, 0), CRootOf(x**5 - x - 1, 1), CRootOf(x**5 - x - 1, 2), CRootOf(x**5 - x - 1, 3), CRootOf(x**5 - x - 1, 4)]

哎呀！SymPy 真是耍赖了。它就说：“你要个封闭形式的答案？没问题啊！我就随便定义个函数叫 CRootOf(x**5 - x - 1, 0)，然后就拿它当答案了。”

这算是作弊，因为它没有回答我们关心的问题。SymPy实际上只是把一个未解决的问题换个新名字，还声称成功了。

当然，SymPy 这样做有它的道理。首先，我们现在很容易找到数值解。

    from sympy import N, CRootOf  # 从 sympy 导入 N 和 CRootOf

    print(N(CRootOf(x**5 - x - 1, 0)))  # 打印出多项式 x^5 - x - 1 的第一个实根的近似值

显示 1.16730397826142

即使没有实数解也能找到解的方案: 多项式方程的一个有趣之处在于，即使没有实数解，你也能总是找到解，至少是数值解！

请看这样一个下面的二次方程，

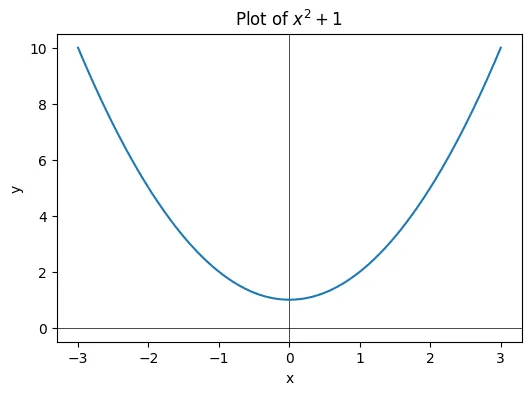
• x 的平方加 1 等于 0

如果画出这个方程，它不会与 (x) 轴相交，表示没有实根。

不过，使用 SymPy，我们可以为任何多项式方程找到数值解，比如说。

from sympy import solve, Eq, CRootOf, N, degree  
from sympy.abc import x  

# 求解方程 x^2 + 1 = 0 的复数根
equation = Eq(x**2 + 1, 0)  
# 计算方程的复数根并计算数值解
numerical_solution = [N(CRootOf(equation, d)) for d in range(degree(equation))]  
# 打印数值解
print(numerical_solution)

这将输出结果是复数列表 [−1.0*I, 1.0*I]。

请注意，这些解使用了 i （虚数单位），这意味着它们是复数解。这体现了代数基本定理，该定理指出，每一个（非常数）多项式方程至少有一个复数解，即使不存在实数解也是如此。

除非在你的领域里复数有实际意义，否则你应该忽略复数解。

总结多项式：

• 四次及以下的多项式方程：总能找到一个包含基本算术运算和根的闭形式解。
• 五次及以上：通常不存在使用基本运算的闭形式解，不过SymPy偶尔也能找到一个。
• 解：多项式总是有解，至少数值上是这样，但这些解可能不是实数（从数学和实际意义上来说）。除非复数在你的领域有意义，否则通常可以忽略它们。

接下来，我们将在方程中加入指数和对数。在解的过程中，我们发现了兰伯特 W 函数 (W 函数)。这是否像 CRootOf 一样是一种捷径？

注：这里的 'x' 通常指代一个变量或特定的函数。

当我们用数学来建模数据时，我们经常使用指数和对数。下面是一个例子，展示了当我们试图用SymPy解这些方程以逆转这些模型时会发生什么：

观察到的:

• 有时你很幸运：第一个方程 x e ˣ =0 有一个初等解 x =0。但这种情况并不总是出现，即使在涉及指数或对数的方程中，有时也可以找到简单的封闭形式解。
• 不过，有两个注意事项：首先，我无法精确定义这个家族，并且不确定是否可以明确定义。其次，求解这些方程需要使用兰伯特 W 函数，例如 W(1) 和 W₋₁(1/10)。当 x 同时出现在指数或对数表达式的内部和外部时，就会出现这种函数。
• 如果你不接受 W ，你就无法用封闭形式解这些方程：这个“家族”的方程通常没有使用兰伯特 W 函数的初等封闭形式解。
• 我们应该接受 W ：兰伯特 W 函数是一个定义明确、易于计算的函数，在数学和科学领域都有广泛的应用。它相比于 exp ， log ， sin 和 cos 的较晚被采用，只是历史的原因。
• 一个 W 可以生成多个解：就像平方根函数那样可以产生两个解一样，一个 W 表达式可以给出零个、一个或两个实数解。当存在两个实数解时，SymPy 会将它们分别列出，一个表示为 W（主分支），另一个表示为 W₋₁（次级分支）。除了实数解之外，任何 W 表达式还会生成无限多个复数解。
• 复数解会出现：有些方程，例如 x log(x)+1=0，只会导致复数解。就像处理多项式一样，除非复数在你的领域中有实际意义，否则可以忽略。
• 五次及以上多项式混合 exp 或 log 仍然无法用初等函数求解：即使使用了兰伯特 W 函数这样的特殊函数，五次及更高次的多项式也无法用初等函数给出封闭形式的解。

同时在方程里用上指数和对数的话，通常找不到解析解，即使用了兰伯特 W 函数也一样。

总之，将指数函数或对数函数与多项式结合通常会使方程无法通过传统的闭式方法求解。然而，如果我们允许使用朗伯 W 函数（也称为朗伯 W 函数），那么仅包含指数或对数，但不同时包含两者 的方程可以求解。我们应该视 W 函数为处理这类问题的有效工具。

接下来，让我们把开普勒问题推广一下，看看加入三角函数后会发生什么。

三角方程

简单的三角函数题： 这是我们的第一批三角函数例题。

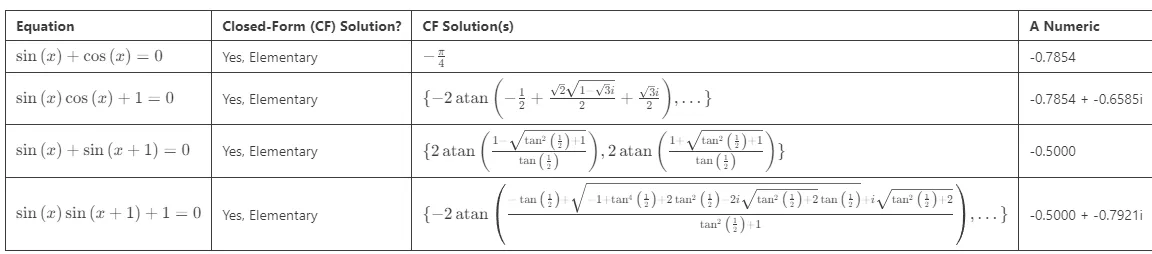
SymPy成功地为每个方程找到了封闭形式的解。这些解涉及三角函数，在某些情况下会出现复数解。（通常我们不会考虑这些复数解，除非它们对问题的实际解决有帮助。）

请记住，正弦和余弦是周期性的，这意味着有无穷多个解。SymPy 提供的解析解通常只表示一个周期中的解。

共频方程式: 在前面的方程式中，我们将三角函数的输入限制为 x +b ，其中 b 是常数。如果我们允许输入如 a ₁ x +b ₁ 和 a ₂ x +b ₂，其中 a ₁ 和 a ₂ 都是有理数，会发生什么？这意味着两个周期函数可能有不同的频率，但这些频率可以同步起来。( a 代表频率。) 我们说这些三角函数具有“共频性”。

观察如下：

• 我们偶尔会得到一个初等函数的解析解。
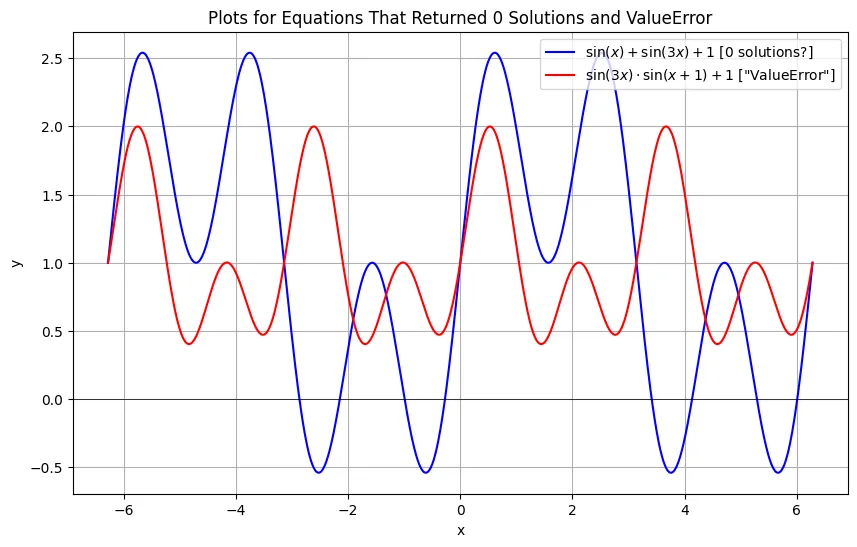
• 对于方程 $\sin(x) + \sin(3x) + 1 = 0$，SymPy 没有找到解。然而，通过数值方法和画图可以发现存在解。另外，当我将该方程输入到在线计算机代数系统 WolframAlpha 中时，它会产生混合解。（WolframAlpha 的解结合了初等函数和六次方程的 CRootOf 表达式。正如我们在多项式部分讨论的那样，这种表达式通常没有封闭形式的解。）
• 当数值方法仍然能提供解时，SymPy 有时会因为寻找封闭形式的解而超时。
• 在其他情况下，它会超时，并且通过数值方法和画图可以确认不存在解。之前，当没有解时，我们得到的是一个复数解。而 WolframAlpha 确实给出了一个复数解。

让我们绘制那个返回零封闭形式解的方程式。还有那个在数值求解时返回 ValueError: 的方程式也来绘制一下。

一些额外的观察

• 从蓝色图表可以看出，SymPy 返回的“无解”消息似乎是一个 bug。图中显然有解，SymPy 应该找到这些解或抛出异常。
• 另一方面，图中确实没有解，ValueError 是准确的。

迄今为止我们遇到的所有三角方程，SymPy 在实数值封闭解存在时似乎都能找到相应解。当这些解不存在时，它会超时退出或给出各种错误。

非公约频率： 在前面的方程式中，我们允许输入形式为 ax + b 的三角函数，其中 a 是有理常数。如果允许输入形式如 a ₁ x +b ₁ 和 a ₂ x +b ₂，其中 a ₁ 是有理数而 a ₂ 是无理数，会发生什么？这意味着这两个周期函数将永远不会同步，无法协同工作。我们说它们具有“非公约频率的”特性。

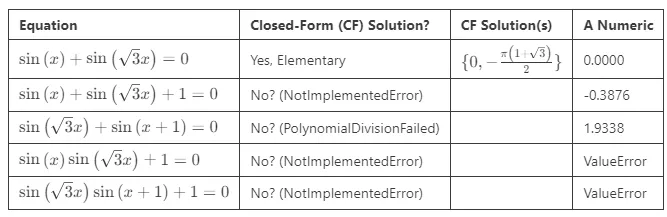
观察如下,

• 具有非共軛频率的两个三角函数的方程一般无法用闭式解表示。当没有基本解时，SymPy 会返回 NotImplementedError ，。
• 我们有时会运气好，偶尔会碰到有基本解的方程。在上面的情况中，SymPy 返回了 PolynomialDivisionFailed ，然而 WolframAlpha 找到了一个闭式解。
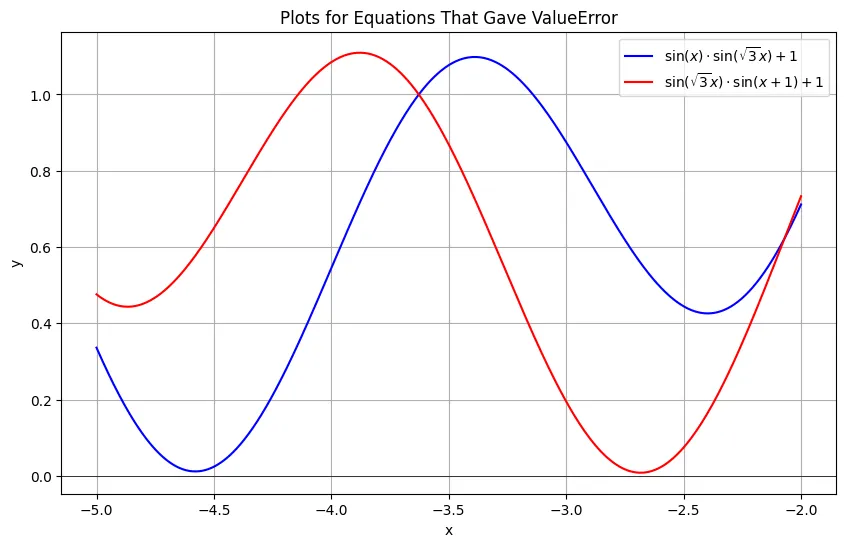
• 当方程无解时，SymPy 会生成 ValueError ，这种情况没有出现复数解，我们可以通过绘图来确认（请参见下图）。

这些方程并不完全为0，因此没有解。

我们的结论是，关于三角方程，我们通常可以找到封闭形式的解。主要的例外似乎是当频率不相容时——比如，在一个方程中同时包含 sin(x) 和 sin(√3 x)。

我们最后要探讨的问题是，当我们将三角函数与指数函数和对数函数结合时会怎样。

我们最后一组样本只需简短讨论即可。如果我们用SymPy运行一组方程样本会怎样？比如，每个方程包含一个三角函数，与其他项结合，这些项可以是x、exp(x)或log(x)。

结果是一致的：SymPy 无法为这些组合中的任何一个方程生成封闭形式的解。然而，对于第一个方程，SymPy 应该得出 x=0 作为封闭形式的解，正如 WolframAlpha 给出的结果一样。

所以，就是这样——对那些通常缺乏封闭形式解的方程进行了一些探讨。如果你想亲自尝试本文中的例子，可以在我的GitHub上的Python代码中找到。

当我处理这些方程例子时，这让我感到惊讶。

• 开普勒方程极为简洁。 我没想到可以用这样的方式来建模椭圆——一个我认为比较复杂的几何形状，以如此优美的方式。
• 兰伯特的 W 函数 对于处理像 x 和 exp⁡(x) 这样的混合项方程非常有用。我们应该把它视为一个基本函数。
• SymPy 是一个出色的免费工具，它可以更好地处理符号代数和三角方程，比我们大多数人手动处理的效果要好得多。虽然在某些情况下可能不如 WolframAlpha，但它非常灵活且易于使用。
• 当混合三角函数 与其他项时，常常导致无法得到封闭形式解，特别是在频率不一致时。
• 当无法得到封闭形式解时，绘图和数值计算方法 就会派上用场，提供实用的结果。

感谢您与我一同踏上这段旅程。希望您现在对何时可以使用方程求解的方法来逆向模型以及SymPy能提供多少支持有了更清晰的了解。此外，当方程无解析解时，您现在也能明白为何需要数值方法以及何时使用。

如果你喜欢用 Python 和 SymPy 来探索 数学，你可能会喜欢用它们来研究 牛顿力学。请参阅这篇 Towards Data Science 文章 以及相关的受欢迎的 PyData 会议演讲。

想看更多文章吗？请在Medium上关注我哦。我写关于Rust和Python、机器学习和统计的文章。我每个月会写一篇文章。