用Python校准市场组合模型：贝叶斯先验的妙用

用户上传的图片

欢迎来到我的系列教程的第二部分，内容是营销组合模型（MMM）。这是一份实用指南，帮助你更好地理解和掌握MMM。在本系列中，我们将探讨模型训练、验证、校准和预算优化等关键问题，全部使用强大的pymc-marketing Python库。无论你是MMM的新手还是想提升技能的老手，本系列将为你提供实用工具和见解，帮助你优化营销策略。

如果你错过了第一集，可以在这里看下：

在这一系列的第二部分中，我们将集中讨论使用实验数据校准模型。

• 为什么校准营销组合模型很重要？
• 我们怎样利用贝叶斯先验值来校准我们的模型？
• 我们可以运行哪些实验来帮助我们确定贝叶斯先验值？

我们将用 Python 和 pymc-marketing 包来完成这个模型的校准，作为结尾。这个模型是在我们之前的第一篇文章里构建的。

你可以在这里查看完整的笔记。

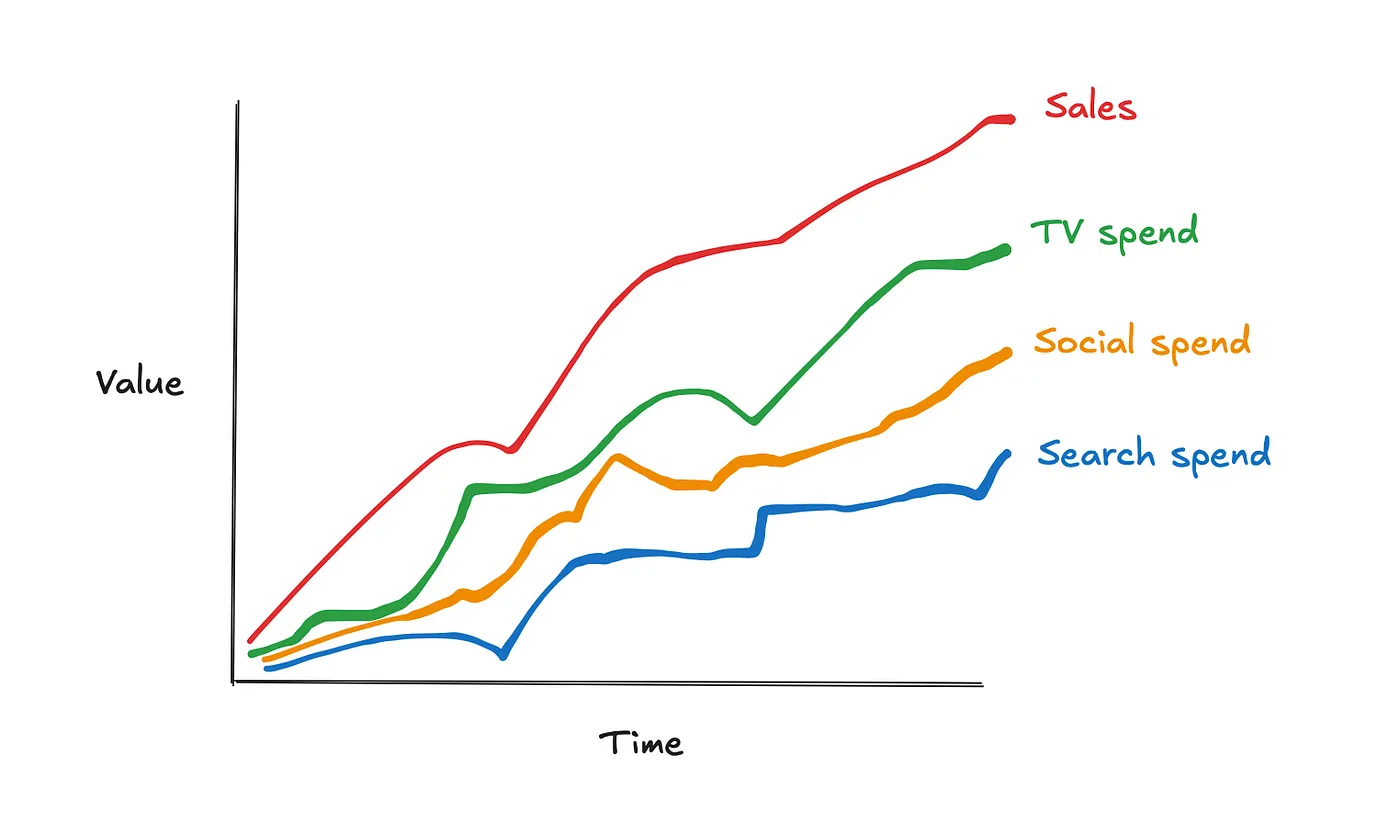
营销组合模型（MMM）是一种统计技术，用于评估不同营销渠道（如电视广告、社交媒体、付费搜索）对销售的效果。MMM旨在了解每个渠道的投资回报率（ROI），并优化未来的营销预算。

有几个原因我们要调整模型。在我们开始Python实操之前，简单聊聊这些原因。

校准MMM非常重要，因为虽然它们提供了很多有用的见解，但仍受到很多因素的限制。

• 多重共线性： 当不同的营销渠道之间高度相关时，就会发生这种情况，使得难以区分它们各自的效应。例如，电视和社交媒体可能同时运行，导致它们影响的重叠。校准通过引入额外的数据或限制条件，帮助我们理清这些渠道的影响。
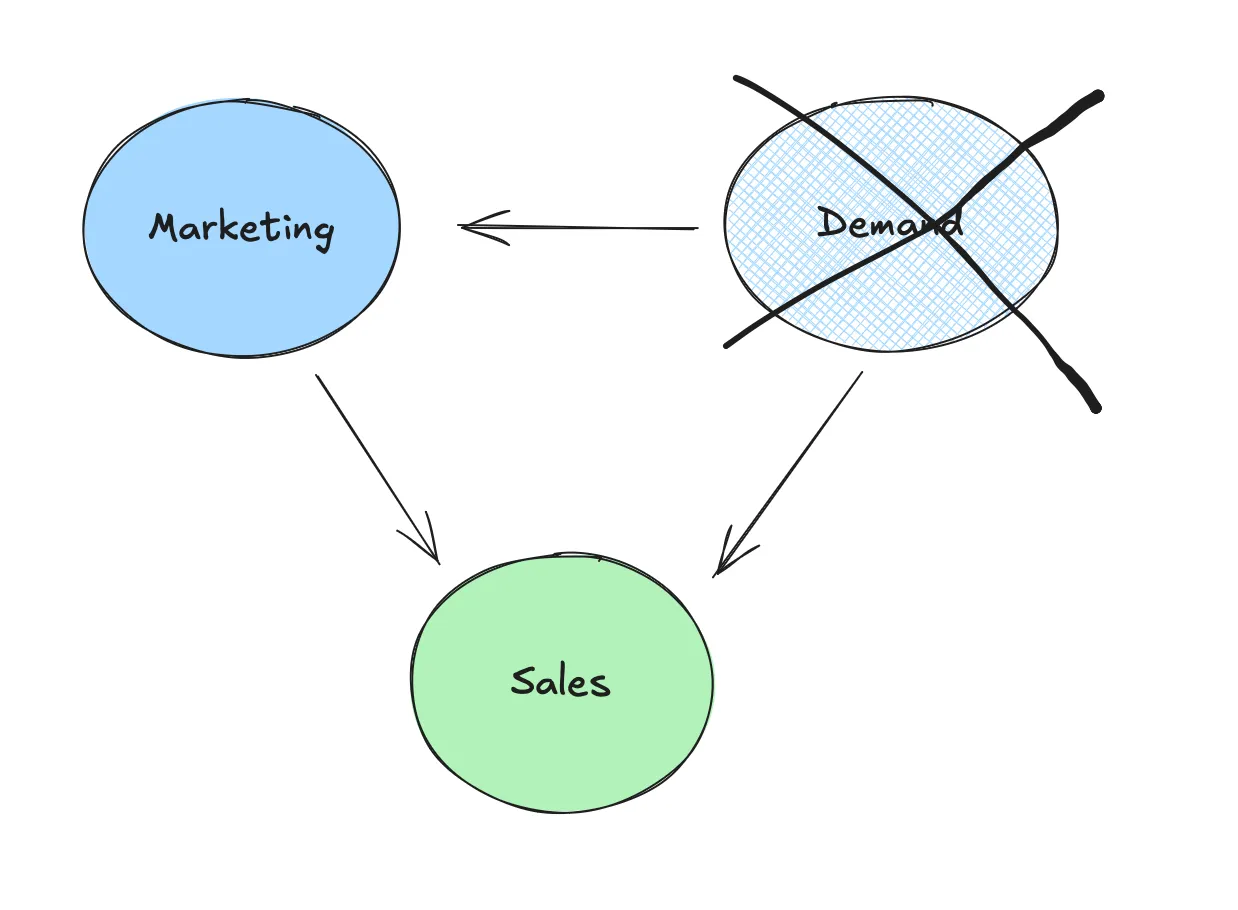
• 未观测到的干扰因素： MMM 模型依赖于观察到的数据，但可能会遗漏一些重要变量，这些变量同样会影响营销和销售，例如季节性或市场需求的变化。校准可以帮助我们纠正这些未被注意到的影响因素。

用户使用excalidraw绘制的图像（excalidraw，一个绘图工具）

• 重新定位的偏误: 你有没有访问过某个产品的网站，然后发现你的所有社交媒体平台突然“巧合地”开始向你展示该产品的广告？这其实是有意为之，我们称这种现象为“重新定位”，并且有时确实能起到效果。事实上，很多被重新定位的潜在客户本就会购买，即使不进行重新定位。

如果没有正确的校准，这些问题可能会导致对营销渠道效果的不准确估计，从而在营销支出和策略的决策上出现失误。

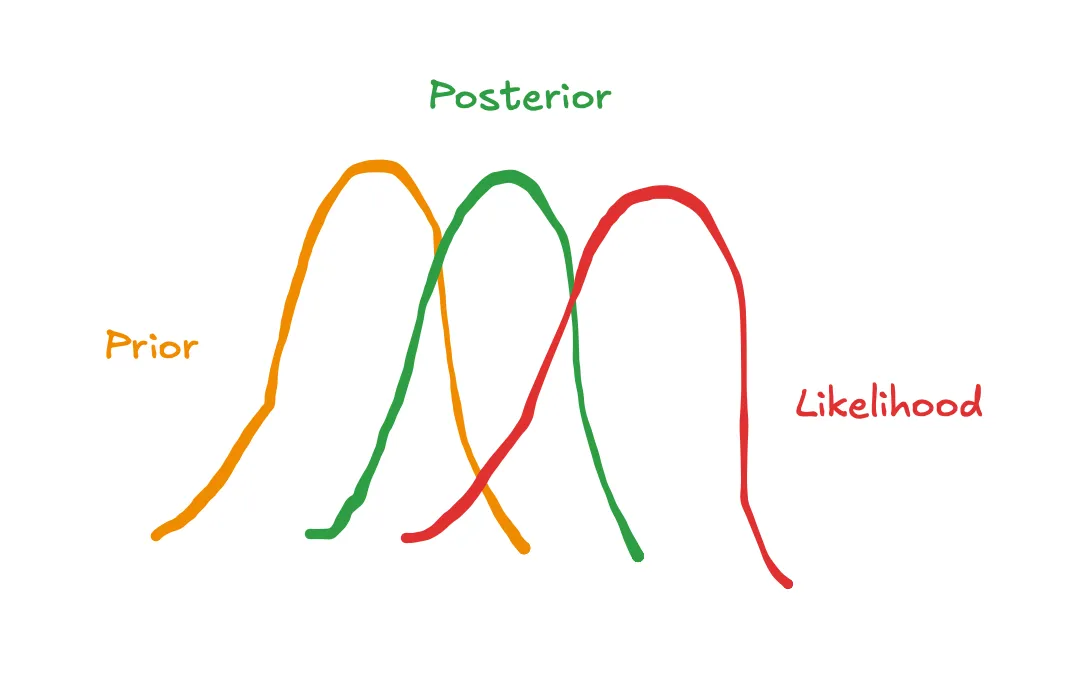
在上一篇文章里，我们讨论了如何用贝叶斯先验表示我们对模型参数的初始信念，例如电视广告支出对销售额的影响力。我们还介绍了pymc-marketing中的默认参数是合理但信息量较弱的选择。提供基于实验的更有信息量的先验可以帮助我们校准模型，并解决上一节提出来的问题。

用户生成的图片（来自Excalidraw）

在 pymc-marketing 中，有几种方法可以设定先验。

• 可以直接像下面的例子这样做，更改默认的饱和度_beta先验，使用截断的正态分布来限制值为正值。请注意，'saturation_beta' 保留英文，因为它看起来像是特定的变量名或参数名。

    model_config = {  
        'intercept': Prior("Normal", mu=0, sigma=2),  
        'likelihood': Prior("Normal", sigma=Prior("HalfNormal", sigma=2)),  
        'gamma_control': Prior("Normal", mu=0, sigma=2, dims="control"),  
        'gamma_fourier': Prior("Laplace", mu=0, b=1, dims="fourier_mode"),  
        'adstock_alpha': Prior("Beta", alpha=1, beta=3, dims="channel"),  
        'saturation_lam': Prior("Gamma", alpha=3, beta=1, dims="channel"),  
        'saturation_beta': Prior("TruncatedNormal", mu=[0.02, 0.04, 0.01], lower=0, sigma=0.1, dims=("channel"))  
    }  

    mmm_with_priors = MMM(  
        model_config=model_config,      
        adstock=GeometricAdstock(l_max=8),  
        saturation=LogisticSaturation(),  
        date_column=date_col,  
        channel_columns=channel_cols,  
        control_columns=control_cols,  
    )

• 使用 add_lift_test_measurements 这个方法，该方法向模型中添加一个新的概率项，有助于校准饱和度曲线，我们会在后续的 Python 教程中详细讲解这一点。

如果你对贝叶斯分析感到不自在，你的替代方案是使用像cvxpy这样的软件包运行带约束的回归作为一种替代方案。下面是一个使用变量系数的上下限来进行约束回归的例子：

    import cvxpy as cp  

    def train_model(X, y, reg_alpha, lower_bounds, upper_bounds):  
        """  
        训练一个带有L2正则化（岭回归）和系数边界约束的线性回归模型。  

        参数：  
        -----------  
        X : numpy.ndarray 或类似  
            特征矩阵，每一行代表一个观测值，每一列代表一个特征。  
        y : numpy.ndarray 或类似  
            回归的目标变量。  
        reg_alpha : float  
            岭惩罚项的正则化强度。较高的值会更严厉地惩罚较大的系数值。  
        lower_bounds : 浮点数列表或None  
            模型中每个系数的下界。如果某个系数没有下界，则将其设置为None。  
        upper_bounds : 浮点数列表或None  
            模型中每个系数的上界。如果某个系数没有上界，则将其设置为None。  

        返回：  
        --------  
        numpy.ndarray  
            回归模型的拟合系数数组。  

        示例：  
        --------  
        >>> coef = train_model(X, y, reg_alpha=1.0, lower_bounds=[0.2, 0.4], upper_bounds=[0.5, 1.0])  

        """  

        coef = cp.Variable(X.shape[1])  
        ridge_penalty = cp.norm(coef, 2)  
        objective = cp.Minimize(cp.sum_squares(X @ coef - y) + reg_alpha * ridge_penalty)  

        # 基于提供的边界创建约束条件  
        constraints = (  
            [coef[i] >= lower_bounds[i] for i in range(X.shape[1]) if lower_bounds[i] is not None] +  
            [coef[i] <= upper_bounds[i] for i in range(X.shape[1]) if upper_bounds[i] is not None]  
        )  

        # 定义并求解该问题  
        problem = cp.Problem(objective, constraints)  
        problem.solve()  

        # 打印优化状态信息  
        print(problem.status)  

        return coef.value

实验可以提供有力的证据来帮助确定MMM中使用的先验。比如，一些常见的实验包括：
（注：MMM即多模式模型（Multi-Modal Model））

用户生成的图片（excalidraw）

• 转化率提升测试 — 这些测试通常在Facebook、YouTube、Snapchat、TikTok和DV360等平台上进行，用户被随机分为测试组和对照组。测试组会接触到营销活动，而对照组不会。通过两组之间转化率的差异，可以评估渠道的实际提升效果。
• 地域提升测试 — 在地域提升测试中，某些地理区域暂停营销活动，而其他区域继续进行。通过对比测试区域和对照区域的表现，可以衡量每个区域营销活动的增量影响。CausalPy Python库提供了一个易于使用的方法，非常值得尝试：

• 切换测试 — 这种方法就是在短时间内快速开启和关闭营销活动，来观察消费者行为的变化。这种方法最适用于那些能立即产生效果的渠道，例如付费搜索。

通过这些实验，你可以获得强有力的实证数据来完善你的贝叶斯先验分布，并进一步提高市场组合模型的准确性和校准。

现在我们知道了为什么需要校准模型，现在我们来校准一下第一篇文章里的那个模型吧。下面我们就来看看具体步骤。

• 模拟数据
• 模拟实验
• 预处理实验数据
• 调整模型
• 验证模型的有效性

我们将从模拟第一篇文章中的数据开始。如果你想了解更多关于数据生成方式的信息，请查看第一篇文章，我们在那里进行了详细的介绍。

当我们训练第一篇文章中的模型时，电视广告、社交媒体和搜索引擎的贡献都被高估了。这似乎是由代理需求没有真正需求那么大所驱动的。所以让我们接着上次的工作继续，想想怎么通过实验来解决这个问题。

为了模拟某些实验结果，我们编写了一个函数，该函数接收已知的通道参数并输出该通道的真实贡献。请记住，在实际情况下我们无法得知这些参数，但这个练习将帮助我们测试并理解来自pymc-marketing的校准流程。

    def exp_generator(起始日期, 时期数, 渠道, adstock_alpha, saturation_lamda, beta, 每周支出, 最大绝对支出, 频率="W"):  
        """  
        生成包含广告积压效应和饱和效应的实验结果时间序列。  

        参数：  
        ----------  
        起始日期 : str 或 datetime  
            时间序列的起始日期。  
        时期数 : int  
            生成的时间序列中的时期数量（例如，周数）。  
        渠道 : str  
            营销渠道的名称。  
        adstock_alpha : float  
            广告积压衰减率，范围在0到1之间。  
        saturation_lamda : float  
            饱和参数（lambda）。  
        beta : float  
            beta系数。  
        每周支出 : float  
            渠道的每周原始支出金额。  
        最大绝对支出 : float  
            用于标准化支出数据的最大绝对支出值，使序列在0到1之间进行归一化。  
        频率 : str，可选  
            时间序列的频率，默认为 'W' 表示每周。遵循 pandas 偏移别名。  
        返回：  
        -------  
        df_exp : pd.DataFrame  
            包含生成的时间序列的DataFrame，包含以下列：  
            - 日期 ：序列中的每个时期日期。  
            - {渠道}_支出原始 ：渠道的原始每周支出。  
            - {渠道}_支出 ：通过 `最大绝对支出` 标准化的渠道支出。  
            - {渠道}_广告积压 ：根据 `adstock_alpha` 进行时间衰减的广告积压转换支出。  
            - {渠道}_逻辑饱和 ：应用 `saturation_lamda` 逻辑饱和后的广告积压转换支出。  
            - {渠道}_销售 ：计算为饱和支出乘以 `beta` 的销售贡献。  

        示例：  
        --------  
        >>> df = exp_generator(  
        ...     起始日期="2023-01-01",  
        ...     时期数=52,  
        ...     渠道="电视渠道",  
        ...     adstock_alpha=0.7,  
        ...     saturation_lamda=1.5,  
        ...     beta=0.03,  
        ...     每周支出：50000,  
        ...     最大绝对支出=1000000  
        ... )  

        """  
        # 0. 创建时间维度  
        日期范围 = pd.date_range(start=起始日期, periods=时期数, freq=频率)  
        df_exp = pd.DataFrame({'日期': 日期范围})  

        # 1. 创建原始渠道支出  
        df_exp[f"{渠道}_支出原始"] = 每周支出  

        # 2. 标准化渠道支出  
        df_exp[f"{渠道}_支出"] = df_exp[f"{渠道}_支出原始"] / 最大绝对支出  

        # 3. 应用广告积压转换  
        df_exp[f"{渠道}_广告积压"] = geometric_adstock(  
            x=df_exp[f"{渠道}_支出"].to_numpy(),  
            alpha=adstock_alpha,  
            l_max=8, normalize=True  
        ).eval().flatten()  

        # 4. 应用逻辑饱和转换  
        df_exp[f"{渠道}_逻辑饱和"] = logistic_saturation(  
            x=df_exp[f"{渠道}_广告积压"].to_numpy(),  
            lam=saturation_lamda  
        ).eval()  

        # 5. 计算销售贡献  
        df_exp[f"{渠道}_销售"] = df_exp[f"{渠道}_逻辑饱和"] * beta  

        return df_exp

下面我们就用这个功能来生成一个为期8周的电视增肌测试的结果。

    # 设置实验生成器所需的参数如下  
    start_date = "2024-10-01"  
    periods = 8  
    channel = "tv"  
    adstock_alpha = adstock_alphas[0]  
    saturation_lamda = saturation_lamdas[0]  
    beta = betas[0]  
    weekly_spend = df['tv_spend_raw'].mean()  
    max_abs_spend = df['tv_spend_raw'].max()  

    df_exp_tv = exp_generator(start_date, periods, channel, adstock_alpha, saturation_lamda, beta, weekly_spend, max_abs_spend)  

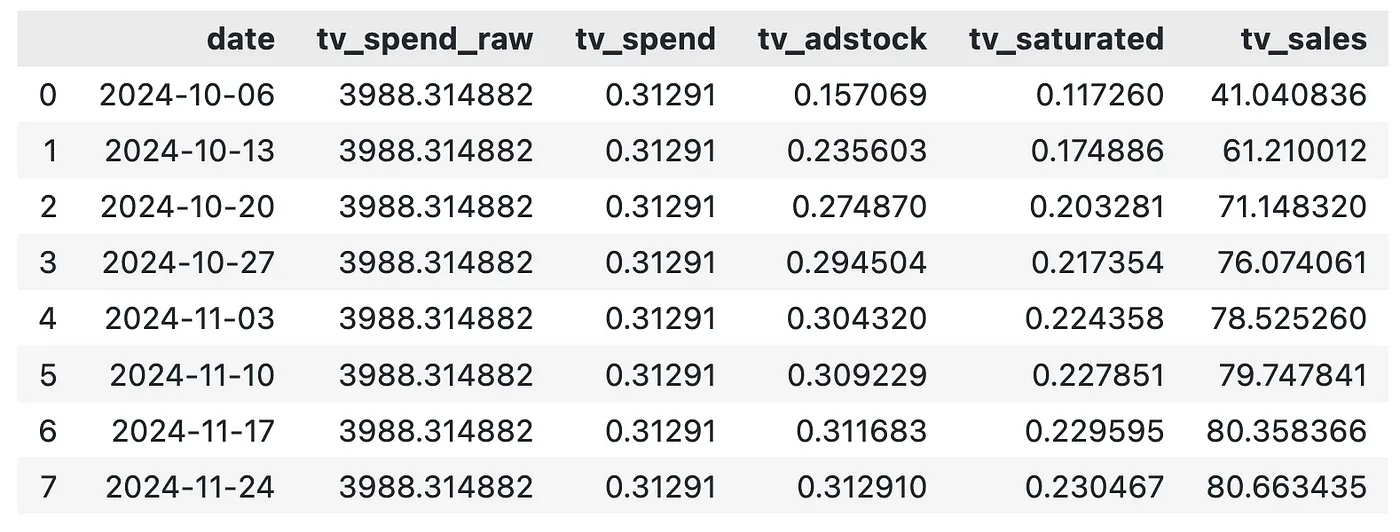
    # 输出生成的实验数据  
    df_exp_tv  

用户生成的图片

虽然我们每周在电视上的花费相同，但电视的贡献会有所变化。这是由广告效果递延效应导致的，因此，我们最好采用每周贡献的平均值。

    周销售额 = df_exp_tv["tv_sales"].mean()  # 计算每周的平均销售额

    # 这里展示计算后的周销售额结果

用户上传的图片

我们现在有了实验结果，需要对它们进行处理，以便按格式添加到模型中。其中每行代表一个实验的数据框，格式如下所示：

• channel：被测试的渠道
• x：测试前的渠道花费
• delta_x：对 x 的调整
• delta_y：由于 delta_x 推断出的销售额变化
• sigma：估计的 delta_y 的标准差

我们没有通过带有不确定性的度量来模拟实验结果中的不确定性，因此将sigma设定为提升值的5%。

# 包裹了每周销售数据的波动和增量计算的DataFrame定义
df_lift_test = pd.DataFrame({  
    "channel": ["tv_spend_raw"],  
    "x": [0],  
    "delta_x": weekly_spend,  # 每周的销售波动
    "delta_y": weekly_sales,  
    "sigma": [weekly_sales * 0.05],  # 每周销售的增量
    }  
)  

df_lift_test

这张图片是用户上传的

在sigma方面，理想的情况是你能够为你的结果的不确定性获得一个度量，这通常可以通过大多数转化率提升或地域提升测试来实现。

我们现在将重新训练那个在第一篇文章中提到的模型。我们将以同样的方式准备训练数据。

• 将数据拆分为特征和目标。为训练数据和非实时数据切片创建索引，这将帮助我们验证模型的效果。

    # 设置日期列  
    date_col = "date"  

    # 设置结果列  
    y_col = "sales"  

    # 设置营销变量  
    channel_cols = ["tv_spend_raw",  
                    "social_spend_raw",  
                    "search_spend_raw"]  

    # 设置控制变量  
    control_cols = ["demand_proxy"]  

    # 创建数据集  
    X = df[[date_col] + channel_cols + control_cols]  
    y = df[y_col]  

    # 设置外部样本长度  
    test_len = 8  

    # 创建训练和测试索引  
    train_idx = slice(0, len(df) - test_len).start + slice(0, len(df) - test_len).stop  
    out_of_time_idx = slice(len(df) - test_len, len(df)).start + slice(len(df) - test_len, len(df)).stop

接着我们加载从第一篇文章保存的模型，并在添加实验结果之后重新训练该模型：

mmm_default = MMM.load("./mmm_default.nc")  # 加载默认的MMM模型
mmm_default.add_lift_test_measurements(df_lift_test)  # 添加提升测试测量
mmm_default.fit(X[train_idx], y[train_idx])  # 对模型进行拟合

这次我们不讨论模型诊断，但如果你想了解的话，可以看看笔记本。

所以让我们来看看这个新模型和实际效果相比如何。下面我们就来瞧瞧真正的贡献值。

channels = np.array(["tv", "social", "search", "demand"])  

true_contributions = pd.DataFrame({'Channels': channels, 'Contributions': contributions})  
true_contributions = true_contributions.sort_values(by='Contributions', ascending=False).reset_index(drop=True)  
true_contributions = true_contributions.style.bar(subset=['Contributions'], color='lightblue')  # 使用浅蓝色
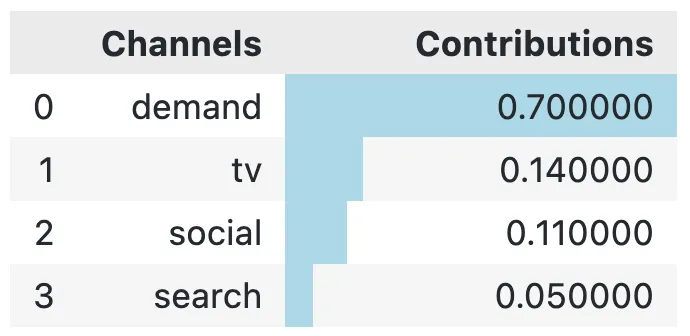
显示 true_contributions

用户分享的图片

当我们比较真正对新模型的贡献时，我们看到电视的贡献现在非常接近于其他贡献（相比之下，我们第一篇文章中的模型，电视的贡献仅为24%！）

    mmm_default.plot_waterfall_components_decomposition(figsize=(10,6)); # 绘制瀑布图分解图，设置图形大小为10x6英寸

用户自己上传的图片

搜索和社交的贡献仍然被高估了，但我们也可以在这里做一些实验来应对这种情况。

今天我们向你们展示了如何通过实验结果来引入先验。pymc-marketing 这个包让分析师在运行模型时更加轻松。如果你想深入了解一下它是如何工作的，可以看看他们的教程：

你可能听说过“所有模型都是错误的，但有些是有用的”这句话。这在很多地方都适用，而且……mmm_lift_test.html
www.pymc-marketing.io](https://www.pymc-marketing.io/en/stable/notebooks/mmm/mmm_lift_test.html?source=post_page-----49dce1a5b33d--------------------------------)

不过，可别被骗了……在让模型变得准确的道路上，你还是得多面对一些难题……

在物流和资源配置方面的挑战，比如你能在多少地理区域或渠道之间进行资源配置的限制，或者在争取营销团队支持新的实验时遇到困难，仅是其中的一些挑战而已。

值得考虑的一点是完全停止市场营销活动一段时间，利用这段时间的结果来预测需求和基本销售额。这有助于解决物流方面的难题，同时也能增强实验的有效性，因为这样可以增强效果。

希望你享受了这篇第二部分的内容！如果你想继续这条掌握MMM的道路，请关注我！在下一篇文章里，我们将开始思考如何更好地优化营销预算！