①课程介绍

课程名称：Python3入门机器学习 经典算法与应用 入行人工智能
课程章节：第六章
主讲老师：liuyubobobo

内容导读

• 第一部分 对四种算法进行效率比较
• 第二部分 一个关于小批量梯度下降的问题

②课程详细

第一部分

这一章的结尾我想对四种算法进行效率与准确率上的比较，批量梯度下降法，随机梯度下降法，小批量梯度下降法，在特征量增大，或者训练量增大的情况下，效率会产生什么样的变化，以此来探究不同算法的应用场景。
导入函数

import numpy as np
import matplotlib.pyplot as plt

数据初始化

np.random.seed(666)
X = np.random.random(size=(10000,10000))

true_theta = np.arange(X.shape[1]+1,dtype=float)
true_theta

X_b = np.concatenate([np.ones((len(X),1)),X],axis=1)

y = X_b.dot(true_theta)

分割数据，并归一化

from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y)

standard = StandardScaler()
standard.fit(X_train)
X_train_standard = standard.transform(X_train)
X_test_standard = standard.transform(X_test)

公式下降法

from nike.LinearRegression import LinearRegression
reg1 = LinearRegression()
%time reg1.fit_normal(X_train_standard, y_train)
reg1.score(X_test_standard, y_test)

批量梯度下降

from sklearn.linear_model import LinearRegression
reg2 = LinearRegression()
%time reg2.fit(X_train_standard, y_train)
reg2.score(X_test_standard, y_test)

随机梯度下降法

from sklearn.linear_model import SGDRegressor
reg3 = SGDRegressor()
%time reg3.fit(X_train_standard, y_train)
reg3.score(X_test_standard, y_test)

小批量梯度下降法

from sklearn.linear_model import BayesianRidge
reg4 = BayesianRidge()
%time reg4.fit(X_train_standard, y_train)
reg4.score(X_test_standard, y_test)

第二部分 一个关于小批量梯度下降的问题

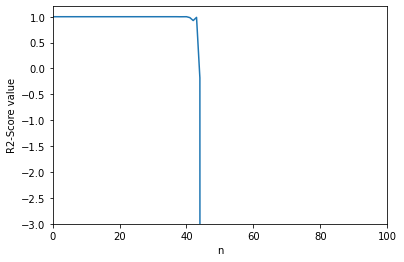
承接上文，在对X的训练量和特征数参数测试效率的过程中，我发现自己实现的小批量梯度下降算法，越来越大的情况下，准确率会极速下降，而sklearn算法则不会影响，我在想我们实现随机梯度下降法的方式是不是有些许问题

def init(m,n):
	#初始化数据
	np.random.seed(666)
	X = np.random.random(size=(m,n))
	true_theta = np.arange(X.shape[1]+1,dtype=float)
	
	X_b = np.concatenate([np.ones((len(X),1)),X],axis=1)
	#对y不加噪点，我觉得数据量可能有点大算的有点慢
	y = X_b.dot(true_theta)
	#归一化+分割数据
	from sklearn.preprocessing import StandardScaler
	from sklearn.model_selection import train_test_split

	X_train, X_test, y_train, y_test = train_test_split(X, y)
	
	standard = StandardScaler()
	standard.fit(X_train)
	X_train_standard = standard.transform(X_train)
	X_test_standard = standard.transform(X_test)
	return	X_train_standard, X_test_standard, y_train, y_test

我自己写的代码小批量梯度下降

score_history=[]
reg1 = LinearRegression()
#将数据从1-100逐级递增，计算代码准确率并记录，用于绘制n与socre的图形
for i in range(1,120):
	X_train_standard, X_test_standard, y_train, y_test=init(1000,i)
	reg1.fit_sgd(X_train_standard, y_train)
    score_history.append(reg3.score(X_test_standard, y_test))
#绘制图形
plt.plot([i for i in range(len(score_history))],score_history)
plt.axis([0,100, -3,1.2])
plt.xlabel('n')
plt.ylabel('R2-Score value')
plt.show()

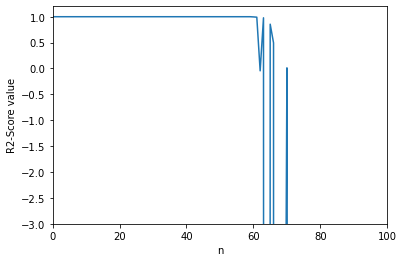
从bobo老师那里复制的小批量梯度下降

score_history=[]
reg2 = LinearRegression2()
#将数据从1-120逐级递增，计算代码准确率并记录，用于绘制n与socre的图形
for i in range(1,120):
	X_train_standard, X_test_standard, y_train, y_test=init(1000,i)
	reg2.fit_sgd(X_train_standard, y_train)
    score_history.append(reg2.score(X_test_standard, y_test))
#绘制图形
plt.plot([i for i in range(len(score_history))],score_history)
plt.axis([0,100, -3,1.2])
plt.xlabel('n')
plt.ylabel('R2-Score value')
plt.show()

#机器学习sklearn
from sklearn.linear_model import SGDRegressor
score_history=[]
reg3 = SGDRegressor()
#将数据从1-120逐级递增，计算代码准确率并记录，用于绘制n与socre的图形
for i in range(1,120):
	X_train_standard, X_test_standard, y_train, y_test=init(1000,i)
	reg3.fit(X_train_standard, y_train)
    score_history.append(reg3.score(X_test_standard, y_test))
#绘制图形
plt.plot([i for i in range(len(score_history))],score_history)
plt.axis([0,100, -3,1.2])
plt.xlabel('n')
plt.ylabel('R2-Score value')
plt.show()

这个问题最后也是bobo老师代为解决的：不是我们的实现“有问题”，而是我们的实现可以更好。但是继续优化这个 SGD 的过程已经不是这个课程的目标了。sklearn 中的 SGD 的原理和我们课程介绍的原理是一致的。但是在细节上，无论是“随机梯度方向的计算”，还是“学习率的自适应变换”，都更加复杂。

第三部分

③课程思考

数据前解释，m=X的训练量，n=X的特征数量
1.m很大 ， n较小(m=1000w,n=10)

• #公式下降: 10.3 s|1.0
• #批量梯度下降:5.86 s|1.0
• #随机梯度下降:46.4 s|0.9999999896236609
• #小批量梯度下降法:10.6 s|1.0

>>在训练量很大的时候且维度较小的时候，使用<公式下降或批量梯度下降或小批量梯度下降法>都是不错的选择

2.m，n都很大(m=10000,n=10000)

• #公式下降:13min 48s|-473.09757045443126
• #批量梯度下降:4min 58s|-12.752179227330855
• #随机梯度下降:34.3 s|-54223552442710.266
• #小批量梯度下降法:6min 6s|0.7442073384872584

>>在训练量和维度都很大的情况下，公式下降法消耗的时间急速上升，准确率下降地很快，使用<批量梯度下降>是更好的选择

3.n很大 ,m较小(m=100,n=10000)

• #公式下降:8min 9s|-5.328102579688343

• #批量梯度下降:137 ms|-0.6312338721134305

• #随机梯度下降:117 ms|-15699348450402.361

• #小批量梯度下降法:1.08 s|-0.002605367097514355

   >>在训练量很小，维度都很大的情况下，，使用<批量梯度下降>是更好的选择
  

总结：在维度小于5000，且m>>n情况使用公式下降法都是很合适的,反之使用批量梯度下降法更好。

④课程截图